سلام دوستان خوبم!حالتون چطوره؟
خودتون میدونید که پیشرفت تو ریاضی چقدر وابسته به تمرین و تکراره!
پس این بار هم همراهمون باشید ^^
معادله چیست؟
مثلا 8=2+χ3 یک معادله است که به ازای 2=χ به یک تساوی عددی تبدیل می شود. ویژگی های یک معادله:
- 1)یک تساوی جبری 2) دارای یک مجهول 3) برقراری تساوی به ازای یک عدد یا بیشتر
به عددی که تساوی به ازای آن برقرار می شود جواب معادله یا ریشه معادله می گویند.
هرمعادله به صورت0 ax + b = را که در آن a و b اعداد حقیقی و a مخالف صفر است، یک معادله درجه اول می نامند. تنها جواب این معادله از x = - به دست می آید.
یادآوری رابطه فیثاغورث: = +
معادله درجه دوم، معادله ای به شکل است0+ bx + c = a که در آن 0 ≠ a ضریب ، b ضریب χ و c عدد ثابت است.
اگر0a×b= باشد نتیجه می گیریم: 0 = a یا 0 = bیا 0= bوa . زیرا حاصل ضرب هر عدد در صفر برایر با صفر است.
معادله شامل عبارت های گویا
معادله گویا چیست؟ معادله ای که مجهول آن در مخرج است.
تابع
مثال: دوچرخه سواری با سرعت ثابت در هر ثانیه 3 متر حرکت می کند.
بین زمان و مسافت رابطه ای وجود دارد. اگر زمان را با χ و مسافت را با y نشان بدهیم، χ٣=y است. متغیر زمان در این مثال به طور مستقل تغییر می کند و متغیر مسافت براساس زمان تغییر می کند. یعنی χ متغیر مستقل و y متغیر وابسته است. این رابطه نوعی رابطه خطی است. به صورت کلی روابطی که به شکل b+χa=y هستند را رابطه خطی می نامیم. اگر رابطه خطی را در یک نمودار بکشیم، به شکل یک خط است.
نمایش تابع به صورت زوج مرتب
χوy را به صورت (χوy) نشان می دهیم. χ را مولفه اول و y را مولفه دوم می نامیم. به دلیل اهمیت ترتیب قرار گرفتن مولفه اول و دوم آن را یک زوج مرتب می نامیم. اگر مولفه های اول دو زوج مرتب برابر بودند، مولفه های دوم نیز باید برابر باشند. در غیر این صورت تابع نیست.
نمایش توصیفی
مثال: برای رابطه χ۵=y به شرطی که χ حتما عدد طبیعی باشد داریم: رابطه ای که به هر عدد طبیعی 5 برابر آن را نسبت می دهد.
نمایش تابع با نمودار وِن
در نمودار وِن، از هر عضو مجموعه A باید فقط یک پیکان خارج شود نه بیشتر. ضمنا اگر از عضوی از مجموعه A پیکانی خارج نشود، آن نمودار نشان دهنده یک تابع نیست. البته اگر پیکانی به عضوی از مجموعه B وارد نشود تاثیری در تابع بودن یا نبودن ندارد.
ضابطه جبری تابع
گاهی می توانیم بین مولفه اول و دوم زوج مرتب یک قانون بیان کنیم. مثال: ...و(8و4)(6و3)(4و2)(2و1)
در این تابع با دو برابر کردن مولفه اول، مولفه دوم به دست می آید. پس داریم:χ۲=y که همان ضابطه جبری تابع است. در نمایش زوج مرتبی مولفه های اول را دامنه تابع و مولفه های دوم را برد می نامیم.
مقدار تابع در یک نقطه
برای این کار باید به ازای همه χ ها عدد مورد نظر را بگذاریم تا مقدار تابع در آن نقطه به دست آید.

تعداد مدادها را x می گیریم. مدادها به خواهر سارا رسیده که می شود χ . پس حالا χ باقی می ماند. سارا نیمی از بقیه که همان χ است را به دوستش داده که این گونه می توان محاسبه کرد:
χ = × χ
پس χ به خواهرش و χ به دوستش رسیده است. حال باید مقداری که برای سارا باقی مانده را به دست بیاوریم: χ = χ + χ
پس میزان سهم خواهر و دوست سارا χ است. پس باقی مانده مدادها که همان سهم ساراست، χاست. طبق گفته سوال تعداد باقی مانده مداد ها 12 تا است. یعنی : 12 = χ
حال با طرفین وسطین مقدار x را به دست می آوریم. یعنی دو طرف را در مخرج کسر که همان عدد 3 است ضرب می کنیم. پس 36=x
بنابراین پاسخ گزینه 2 است.
معادله زیر را به روش تجزیه با کمک اتحاد مزدوج حل کنید.
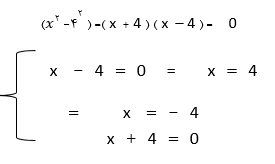

خب خسته نباشید.توی فایل ضمیمه ما نکات بیشتری از این مبحث رو براتون آماده کردیم.
راستی دفترچه جامع 18 آذر رو یادتون نره!پز از نکات آموزشی و تست های مشابه آزمونتونه که حلش حتما توصیه میشه!


