سلام به همه نهمی های عزیز 🖐🖐
در این مطلب به فصل چهارم کتاب ریاضی نهم میپردازیم.

🔴ویژگیهای مطلب🔴
درسنامه کامل و نکات
مثال های فراوان
پاسخ کلیدی و تشریحی در فایل ضمیمه
توان : اگر عددی چند بار در خودش ضرب شود برای خلاصه نویسی از توان استفاده می شود.
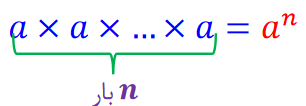
ضرب اعداد توان دار :
الف) اگر پایه ها برابر باشند : یکی از پایه ها را نوشته و توان ها را با هم جمع می کنیم.
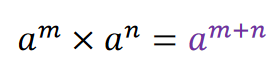
ب) اگر توان ها برابر باشند : یکی از توان ها را نوشته و پایه ها را در هم ضرب می کنیم.
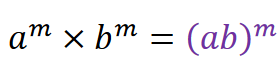
تقسیم اعداد توان دار :
الف) اگر پایه ها برابر باشند : یکی از پایه ها را نوشته و توان ها را از هم کم می کنیم.
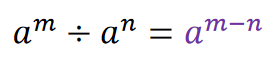
ب) اگر توان ها برابر باشند : یکی از توان ها را نوشته و پایه هارا بر هم تقسیم می کنیم.
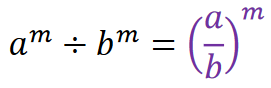
توان منفی : برای به دست آوردن توان منفی عدد پایه را معکوس کرده تا به توان مثبت تبدیل شود.
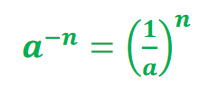
نکته : هر عدد (غیر از صفر) به توان صفر باشد حاصل عدد یکاست.
مثال : حاصل عبارت مقابل را به دست آورید؟
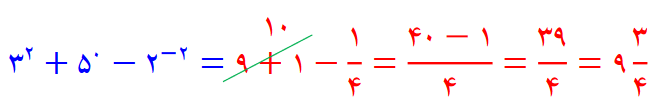
نماد علمی: برای محاسبه ساده تر اعداد خیلی بزرگ و اعداد خیلی کوچک آن ها را به صورت توانی از عدد 10 می نویسیم.
نکته : به طور کلی نماد علمی هر عدد اعشاری مثبت به صورت است که در آن a عددی بین 0 و 10 هست و n هر عدد صحیحی است.
الف) نماد علمی اعداد توان مثبت:
ابتدا یک رقم از سمت چپ جدا کرده سپس به تعداد رقم های بعد از ممیز توانی از عدد 10 می نویسیم.
ب) نماد علمی اعداد توان منفی :
ابتدا یک رقم مخالف صفر از سمت چپ جدا کرده سپس به تعداد رقم های قبل از ممیز توانی از عدد 10 می نویسیم.
مثال : حاصل عبارت زیر را به صورت نماد علمی بنویسید.
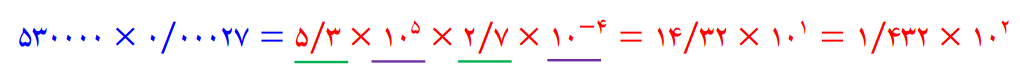
ریشه گیری :
الف) ریشه دوم اعداد : هر عدد دارای دو ریشه دوم است :(یکی مثبت و دیگری منفی)
ب) ریشه سوم اعداد : هر عدد دارای یک ریشه سوم است.
نکته : اگر 𝒂 یک عدد حقیقی باشد ریشه سوم آن را به صورت نشان می دهیم.
نکته : اعداد منفی جذر (ریشه دوم) ندارند.
ضرب و تقسیم رادیکال ها :
اگر دو رادیکال دارای ریشه (فرجه) یکسان باشند می توانیم آن ها را در هم ضرب یا بر هم تقسیم کنیم.
نکته : اگر رادیکال ها دارای عدد صحیح باشند ابتدا اعداد صحیح را ضرب یا تقسیم کرده سپسرادیکال ها راضرب یا تقسیم می کنیم.
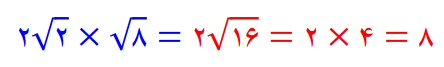
ساده کردن رادیکال ها :
بعضی از رادیکال ها را می توان ساده کرد.به اینصورت که برای عدد یک ضربی بنویسیم که یکی از آن اعداد ریشه دوم یا ریشه سوم داشته باشد.
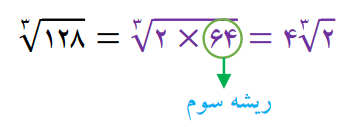
جمع و تفریق رادیکال ها :
اگر قسمت رادیکال ها پس از ساده کردن مثل هم باشند می توانیم آن ها را همانند عبارت های جبری با هم جمع یا تفریق کنیم.
گویا کردن مخرج کسرهای رادیکالی :
گاهی اوقات برای ساده کردن الزم است مخرج کسر را از حالت رادیکالی بیرون بیاوریم که برای این کار صورت و مخرج را در عددی ضرب می کنیم تا مخرج از حالت رادیکالی خارج شود.
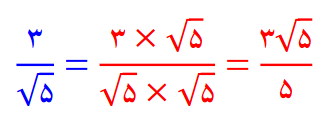
و حالا وقته تسته!!!



برای ارتباط با پشتیبان ویژه و اطلاع از شرایط مشاوره با رتبه هاي برتركانوني
به لينك زير مراجعه كنيد.


