سلام به همه هفتمی های عزیز 🖐🖐
در این مطلب به فصل چهارم کتاب ریاضی هفتم میپردازیم.

🔴ویژگیهای مطلب🔴
درسنامه کامل و نکات
مثال های فراوان
پاسخ کلیدی و تشریحی در فایل ضمیمه
انواع خط:
1.خط راست: خطی است که ابتدا و انتها ندارد و خط را با حروف کوچک انگلیسی نامگذاری می کنند:

2. خط شکسته :

3. خط خمیده:

پاره خط :
خطی است (خط راست) که از دو طرف بسته (محدود) باشد و پاره خط را با حروف بزرگ انگلیسی نام گذاری میکنند.
نیم خط :
خطی است (خط راست) که از یک طرف بسته و از یک طرفباز باشد و نیم خط را از طرفی که بسته است با حرف بزرگ و طرفی که باز است با حرف کوچک نام گذاری می کنند .
نکته :
برای به دست آوردن تعداد نیم خط ها اگر نقاط روی یک خط قرار داشته باشند از رابطه ی زیر استفاده می کنیم :
تعداد نیم خط ها=تعداد نقاط * 2
(برای استفاده از روش تشریحی کامل مثال ها میتونید جزوه این فصل را در بخش فایل های ضمیمه دانلود بفرمایید!!!)
زاویه :
از برخورد دو نیم خط در یک نقطه زاویه تشکیل می شود و به نقطه ی برخورد راس زاویه می گویند.
🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴
انواع زاویه :
- زاویه تند یا حاده :
- اندازه ی آن از 90درجه کمتر است.
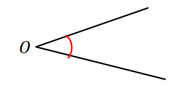
- زاویه راست یا قائمه :
- اندازه ی آن90 درجه است.
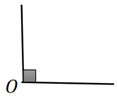
- زاویه باز یا منفرجه :
- اندازه ی آن از90 درجه بیشتر و از180 درجه کمتر است.
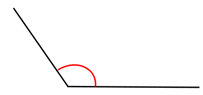
- زاویه نیم صفحه :
- اندازه ی آن180 درجه است.
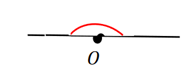
دو زاویه متقابل به راس :
دو زاویه ای که راس مشترک دارند و اضالع آن در امتداد هم باشند.
نکته : زاویه های روبه رو در متقابل به راس برابر و زاویه های مجاور مکمل (180درجه) هستند.
نکته : برای به دست آوردن تعداد زاویه ها در یک شکل از همان رابطه ی تعداد پاره خط ها استفاده میکنیم.
دو زاویه متمم : دو زاویه ای که مجموع آن ها90 درجه باشد.
دو زاویه مکمل : دو زاویه ای که مجموع آن ها180 درجه باشد.
دو زاویه مجاور : دو زاویه ای که راس و یک ضلع مشترک داشته باشند.
دو زایه مجانب : دو زاویه ی مجاوری که مجموع آن ها180 درجه باشد.
(برای استفاده از روش تشریحی کامل مثال ها میتونید جزوه این فصل را در بخش فایل های ضمیمه دانلود بفرمایید!!!)
انواع چند ضلعی ها :
1) چند ضلعی محدب: چند ضلعی که تمام زاویه های آن کمتر از180درجه باشد.
2) چند ضلعی مقعر: چند ضلعی که حداقل یکی از زاویه های آن از180 درجه بیشتر باشد.
3) چند ضلعی منتظم: چند ضلعی که تمام اضلاع و تمام زاویه های آن برابر باشند.
(برای استفاده از روش تشریحی کامل مثال ها میتونید جزوه این فصل را در بخش فایل های ضمیمه دانلود بفرمایید!!!)
انواع تبدیلات هندسی :
انتقال : وقتی شکلی را در صفحه انتقال دهیم تصویر به دست آمده مساوی و هم جهت شکل اولیه است.
تقارن : وقتی قرینه یک شکل را نسبت به یک خط پیدا کنیم تصویر به دست آمده مساوی آن ولی جهت آن تغییر می کند.
دوران : در دوران یک شکل باید مرکز دوران وجهت دوران ومقدار درجه مشخص شود.
شکل های مساوی (هم نهشت) : اگر شکلی را با یک یا چند تبدیل (انتقال و تقارن یا دوران) در صفحه برشکل دیگر منطبق کنیم. آن دو شکل با هم مساوی (هم نهشت) هستند.
نکته : دردو شکل هم نهشت اجزای متناظر دو شکل (اضلاع و زاویه ها) با هم برابرند.
و حالا وقت تسته :)





برای ارتباط با پشتیبان ویژه و اطلاع از شرایط مشاوره با رتبه هاي برتركانوني
به لينك زير مراجعه كنيد.


