فضای سه بعدی - خلاصه نکات - هندسه دوازدهم - فاضل مهرآئین

سلام دوستان ! ✋

در این مطلب قصد داریم بخش فضای سه بعدی از مبحث بردارها را در قالب درسنامه و تست بررسی کنیم.

در این مطلب پنج تست از مبحث فوق قرار دادیم .

 اگر سوالی از این مطلب دارید در قسمت کامنت ها بپرسید .

برای دریافت پاسخ تشریحی ، مطلب را از قسمت فایل های ضمیمه دانلود کنید.

فاضل مهرآئین _ دانشجوی مهندسی مکانیک صنعتی شریف _ رتبه 333 منطقه یک

برای ارتباط بیشتر با برترها و رزرو پشتیبان ویژه، رتبه برترهای کانون قلمچی را دنبال کنید، 

همچنین می توانید با شماره ۰۲۱۸۴۵۱ داخلی ۳۱۲۳ تماس بگیرید.

هر نقطه از صفحه مختصات را به صورت زوج مرتب (x,y) نمايش مي‎دهند در اين صورت این مجموعه که x,y از اعداد حقیقی هستند، شامل همه نقاط صفحه مختصات ميباشد و آن را با  R^2 نمايش ميدهند.

دستگاه مختصات سه بعدي: در دستگاه مختصات سه بعدي، سه مولفه طول، عرض و ارتفاع داريم؛ يعني دستگاه مختصات سه بعدي شامل ox ، oy، oz است و هر نقطه آن به شكل (x,y,z) نمايش داده ميشود. در دستگاه مختصات سه بعدي محورهایox ،oy ،oz  دو به دو بر هم عمودند وبردارهايi ،j ،k بردارهاي يكه محورها ميباشند. دستگاه مختصات سه بعدي، يک دستگاه راست گرد ( جهت مثلثاتي) است كه ميتوان جای x ، y وz  را با رعايت ترتيب آنها ( اولx ، بعدy  و سپسz ، در جهت مثلثاتي) عوض كرد. از برخورد هر دو محور يک صفحه تشكيل شده است. صفحات مورد نظر xoy ،xoz ،yoz  هستند. 

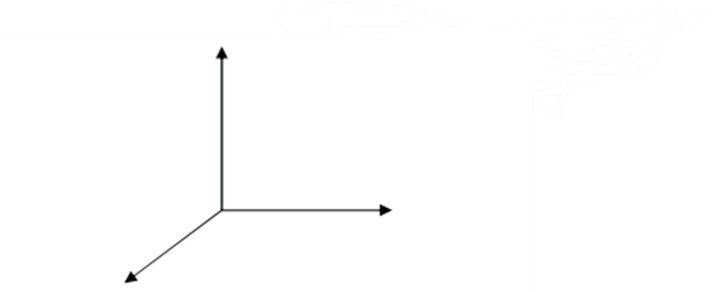
محورها فضا را به به هشت ناحيه تقسيم ميشود كه چهارتاي آن بالاي صفحه xoy  و چهار تاي آن پايين صفحه xoy قرار ميگيرد و مانند دستگاه مختصات دو بعدي شماره گذاري ميشود. 

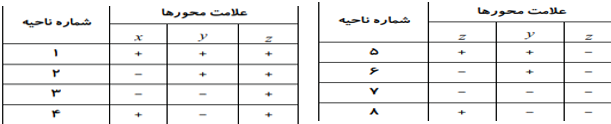
تصوير و قرينه ي يك نقطه نسبت به صفحات و محورهاي مختصات: 
 
 الف) در تصوير روي محور يا صفحات مختصات، مولفه هاي محور يا صفحات ذكر شده را ثابت نگه ميداريم و بقيه مولفه ها صفر ميشوند. 
 
 ب) در قرينه نسبت به محور يا صفحات مختصات، مولفههاي محور يا صفحات ذكر شده را ثابت نگه ميداريم و بقيه مولفهها قرينه ميشوند. 

اصل نقطه از صفحات و محورهاي مختصات: 

براي محاسبه فاصله نقطه A{x1 ,y1 ,z1}تا محورهاي مختصات يا صفحات مختصات، بايد مولفه ذكر شده را در رابطه زیر صفر قرار دهیم.

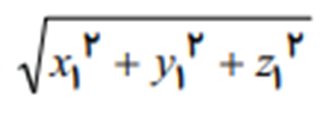
اگر A(x 1 ,y 1 ,z 1) و B(x 2 y2  z 2) دو نقطه در فضا باشند،

1. فاصله لین دو نقطه در فضا برابر است با:

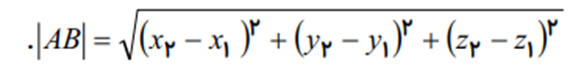
2. مختصات نقطه M وسط پاره خط AB  به صورت زیر میباشد.

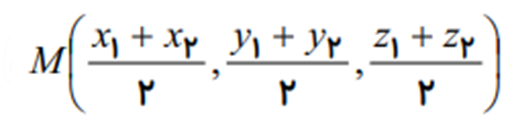
نكته: مركز ثقل (نقطه گرانيگاه) مثلث ABC را با نماد G نشان داده و محل برخورد ميانه ميباشد. مختصات G از رابطه به دست مي آيد.

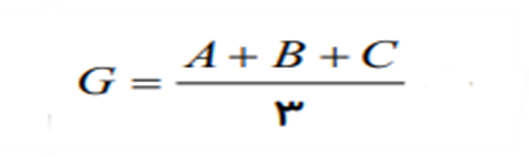
نكته: مي دانيم در متوازي الاضلاع قطرها يكديگر را نصف ميكنند؛ پس بين مختصات رئوس متوازي الاضلاع ABCD ، رابطه A + C = B + D برقراراست. 

ضرب عدد در بردار:

 براي ضرب عدد حقيقي k  در بردار(a1 ,a2, a3)  کافی است عدد k را در تک تک مولفه ها ضرب کنیم. اگر k مثبت باشد آن گاه ka  و aهم جهت هستند و اگر k منفی باشد خلاف جهت هستند. پس میتوان گفت دو بردار زمانی موازی هستند که مضرب هم باشند.

جمع دو بردار:

جمع دو بردار را از دو رويكرد تحليلي و هندسي بررسي ميكنيم. 

1. تحلیلی: برای جمع دو بردار طول ها با هم عرض ها با هم و ارتفاع ها با هم جمع میشوند.

2. هندسی: دو روش زیر وجود دارد

الف) روش مثلثي: زماني از اين روش استفاده ميشود كه دو ( يا چند) بردار، پشت سر هم باشند. يعني انتهاي بردار قبلي، ابتداي بردار بعدي باشد. در اين روش، مجموع بردارها از وصل كردن ابتداي بردار اول به انتهاي بردار آخر به دست مي آيد.

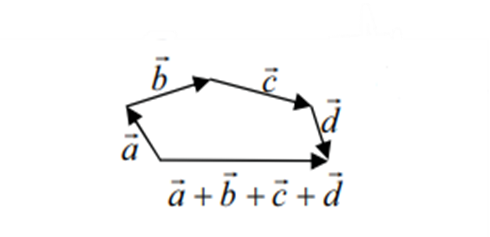
ب) روش متوازی الاضلاع:وقتي دو بردار، هم مبدا ( هم راس) باشند، براي جمع از روش متوازي الاضلاع استفاده ميكنيم. در اين روش از انتهاي هر بردار، موازي و هم ارز بردار ديگر رسم ميكنيم، قطر متوازي الاضلاع كه ابتداي آن راس مشترك دو بردار است، جمع دو بردار را نشان ميدهد.

تفریق دو بردار: برای تفریق نیاز نیست چیزی بیاموزید تفریق همان جمع است با این فرض که باید با قرینه بردار دوم جمع کنید.

بردار يكه: بردار به طول يك بردار يكه ناميده ميشود. برداري به طول يك و در جهت بردارمی باشد. بردارهای یکه محورهای مختصات به ترتیب  i(1,0,0) و j(0,1,0) وk(0,0,1) میباشند.

تست ها 

در شکل مقابل، طول یال مکعب 2 واحد است. مختصات کدام نقطه درست است؟ ( تالیفی – آسان)

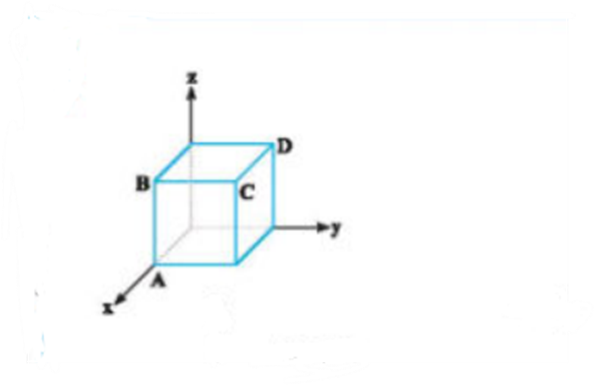
1) A(2,0,0)

B(2,0,2) (2

C(2,2,2) (3

D(2,2,0) (4

دو نقطه A(-1,1,a) و B(b,1,-2)نسبت به یکی ازمحورهای مختصات، قرینه یکدیگرند. حاصل a+b  کدام است؟ ( تالیفی - آسان)

1)1

2)1-

3)3

4)3-

نقطه A(a,b,4) بر روی خط گذرنده از دو نقطه (0,1,2) و (1,-1,0) واقع است. دوتایی مرتب (a,b) کدام است؟ (کنکور نظام قدیم – آسان)

1. (3 و 1-)

2. (2 و 1-)

3. (2- و 1)

4. (3 و 1)

در مستطیل ABCD  حاصل جمع دو بردار DA و CA کدام است؟ ( کنکور نظام قدیم - متوسط)

1. 2BC

2. O

3. 2DA

4. 2AB

نوع مثلث ABC به رئوسA(0,2,-1) B(2,2,3) C(-2,-1,5)، کدام است؟ (مشابه تمرین کتاب درسی - متوسط)

1. متساوی الساقین

2. قائم الزاویه

3. قائم الزاویه متساوی الساقین

4. نامشخص

پاسخ تست ها در فایل ضمیمه آورده شده است.