سلام به همه دوستان هشتمی عزیز !
در این مطلب قصد داریم نکات مهم درس 6 و 7 ریاضی هشتم را با هم مطالعه و بررسی کنیم.
امیدواریم مطالب بیان شده، شما را در یادگیری این مباحث، یاری کند.
برای دریافت کامل این مطلب با گرافیک و کیفیت بهتر ، فایل پی دی اف را از قسمت ضمیمه دانلود کنید.
الهه پروری فارغ التحصیل مهندسی شیمی دانشگاه تهران

صفحه اینستاگرام ما
برای ارتباط با برترها و رزرو پشتیبان ویژه پیج کانون برترها را دنبال کنید.
همچنین میتوانید با شماره ۰۲۱۸۴۵۱ داخلی ۳۱۲۳ تماس بگیرید.
همنهشتی مثلث های قائم الزاویه
دو حالت دیگر برای همنهشتیِ دو مثلث قائم الزاویه:
- برابری وتر و یک ضلع ( و ض )
- برابری وتر و یک زاویۀ تند ( و ز )
*سوال 1: پاره خط AH، ارتفاع وارد بر قاعدۀ مثلث متساوی الساقین ABC است.
چرا مثلث های ایجاد شده با یکدیگر همنهشت اند؟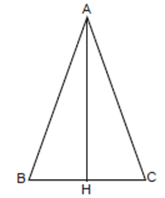
پاسخ:
در مثلث متساوی الساقین ارتفاع وارد بر ساق، عمود بر ساق می باشد، پس در نتیجه دو مثلث ایجاد شده قائم الزاویه میباشند. همچنین در مثلث متساوی الساقین دو ساق مثلث با هم برابر است و این ساق ها وترهای مثلث های ایجاد شده می باشند. پس دو مثلث ایجاد شده با حالت ( و ض) با هم همنهشت اند.
*سوال 2: از نقطه M، وسط پاره خط AB بر دو خط موازی a و b عمود رسم کرده ایم. دو مثلث ایجاد شده به چه حالتی با یکدیگر همنهشت اند؟
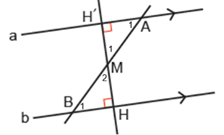
پاسخ:
دو خط a و b موازی و پاره خط AB مورب ، در نتیجه دو زاویه A1 و B2 با هم برابرند.
و طبق صورت سوال دو پاره خط AM و BM با هم برابرند. در نتیجه دو مثلث به حالت ( و ز ) همنهشت اند.
*سوال 3 : در مربع ABCD ، نقطه های E و F به ترتیب روی اضلاع BC و AB قرار دارند به طوری که AE = FC . اگر BAE=15 درجه، آنگاه زاویه CFE چند درجه است؟
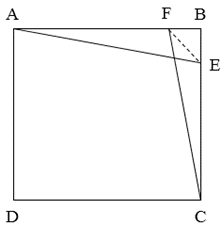
پاسخ :
دو مثلث ABE و BCE به حالت ض ز ض همنهشت اند. پس در نتیجه دو ضلع AB = BC
در نتیجه مثلث BEF قائم الزاویه متساوی الساقین است. و چون دو مثلث ABE و BCE همنهشت اند پس زاویه BCF = 15 و زاویه BFC = 75 درجه می باشد. در نتیجه زاویه CFE برابر با 30 درجه می باشد.


موفق باشید...


