دانش آموزان عزیز سلام
در این سری مطالب میخواهیم در چندبخش، مبحث تابع در سه سال دبیرستان را به طور کامل پوشش دهیم .
امیدوارم که این مطالب برای شما مفید باشد.
🟣ویژگی های مطلب🟣
1- درسنامه کامل به همراه مثال و نکات تابع
2- 5 تست شناسنامه دار از این مبحث
3-پاسخ کلیدی تست ها در انتهای مطلب
4- ویدئو و تدریس پاسخ تشریحی تست ها
 | مولف: سروش اسماعیلی رتبه 395 کنکور ریاضی 1402 دانشجوی مهندسی مکانیک دانشگاه تهران |
در ابتدا سوالات مهمی که از این بخش در امتحانات نهایی 1404 آمده است را مرور میکنیم تا اهمیت مبحث درک شود.
سوالات تابع دوازدهم خرداد 1404

حال به سراغ درسنامه تابع میرویم
بخشی از درسنامه تابع در زیر آمده:
نکات توابع صعودی و نزولی
•اگر f روی بازهای صعدی اکید باشد پس صعودی نیز است(همینگونه برای نزولی)
•هر تابع اکیدا یکنوا، یک به یک و در نتیجه وارونپذیر است.
•هر تابع یک به یک قطعا یکنوا نیست، اما اگر یک به یک و پیوسته باشد اکیدا یکنوا نیز است.
•اگر f صعودی(نزولی) باشد، -f نزولی(صعودی) است
•اگر دو تابع f,g هر دو صعودی باشند، f+g نیز صعودی است اما یکنوایی f-g،f×gو f/g مشخص نیست.
•توابع چندجملهای درجه زوج یکنوا نیستند.
•توابع f وf-1 هم جهتاند یعنی اگر f اکیدا صعودی(نزولی) باشد وارونش نیز اکیدا صعودی(نزولی) است.
•اگر f اکیدا صعودی باشد، محل تلاقی آن با تابعf-1 در صورت وجود روی خط y=x خواهد بود و میتوان برای پیدا کردن آن نقطه به جای حل معادله f(x)=f-1(x) معادله f(x)=x را حل کرد!
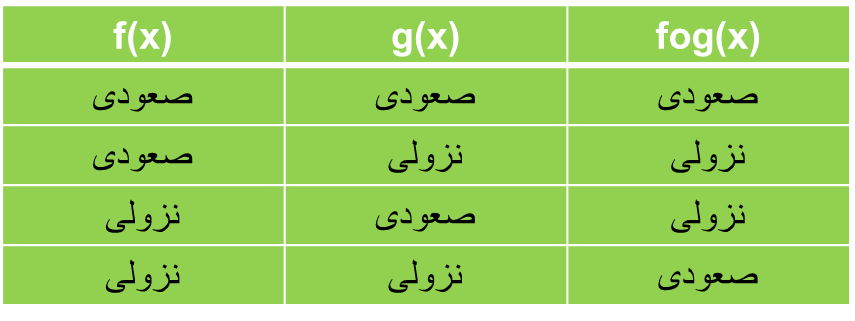
صعودی و نزولی در ترکیب توابع
با استفاده از جدول زیر یکنوایی ترکیب دو تابع f,g را نتیجه میگیریم:
🔵برای مطالعه ادامه درسنامه لطفا جزوه را از فایل ضمیمه دانلود کنید 🔵
🔵عضویت در کانال تلگرام کانون برترها🔵


