سلام به همه هشتمی های عزیز 🖐🖐
در این مطلب به فصل نهم کتاب ریاضی هشتم میپردازیم.

🔴ویژگیهای مطلب🔴
درسنامه کامل و نکات
مثال های فراوان
پاسخ کلیدی و تشریحی در فایل ضمیمه
دایره : به مجموعه نقاطی که از یک نقطه مشخص(مرکزدایره)، به یک اندازه باشند.
نکته : دایره را اختصار به صورت 𝒄(𝒐 , 𝒓) نشان می دهند.
اجزای دایره :
1) شعاع دایره : فاصله ی مرکز دایره تا محیط دایره را شعاع و با حرف(𝒓 یا 𝑹)نشان می دهند.
2) کمان دایره : فاصله ی ایجاد شده روی محیط دایره را کمان و با دو حرف و سه حرف نشان می دهند.
3) وتر دایره : پاره خطی که دونقطه ی روی محیط دایره را به هم وصل کند وتر و با دو حرفنشان می دهند.
4) قطر دایره : پاره خطی است که دو نقطه ی روی محیط دایره را به هم وصل می کند و از مرکز دایره می گذرد. قطر را با دو حرف نشان می دهند.
نکته : بزرگترین وتر دایره ،قطرنام دارد. و قطر 2 برابر شعاع است.
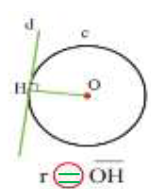
وضعیت خط و دایره :
خط و دایره دارای سه وضعیت هستند :
1) خط ممکن است بیرون از دایره باشد. در این حالت خط و دایره نقطه مشترک(برخورد) ندارند.

2) خط ممکن است داخل دایره باشد. در این حالت خط و دایره دو مشتــــرک(برخورد) دارند.

3) خط ممکن است مماس (چسبیده) بر دایره باشد. در این حالت خط و دایره یک مشترک(برخورد) دارند.
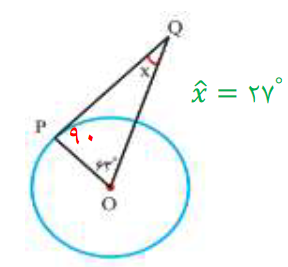
مثال : با توجه به شکل زاویه ی خواسته شده چند درجه است؟
پیدا کردن مرکز دایره :
ابتدا دو وتر غیر موازی رسم می کنیم. سپس عمود منصف های آن دو وتر را رسم کرده که محل برخورد آن دو عمود منصف مرکز دایره نام دارد.
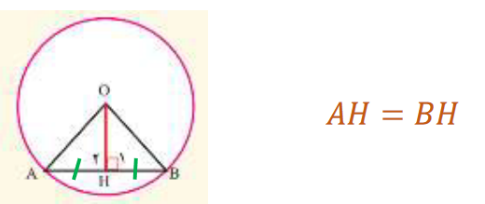
نکته : خطی که از مرکز بر وتر عمود باشد آن را به دو قسمت مساوی تقسیم می کند. و بر عکس خطی که از وسط وتر و مرکز دایره بگذرد ، بر وتر عمود است.
زاویه مرکزی : زاویه ای است که رأس آن مرکز دایره و دو ضلع آن شعاع دایره باشد.
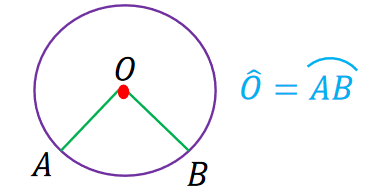
اندازه ی زاویه مرکزی : زاویه ی مرکزی برابر است با اندازه ی کمان روبه رو آن.
نکته : اگر دو کمان مساوی باشند وترهای نظیرآن دو کمان نیز برابرند و برعکس.
تقسیم دایره به کمان های مساوی :
ابتدا یک شعاع دایره رسم می کنیم سپس محیط دایره(360درجه) را بر تعداد کمان های خواسته شده تقسیم کرده ،
نقاله را منطبق بر شعاع گذاشته و زاویه مورد نظر را مشخص می کنیم و در آخر دهانه ی پرگار را به اندازه ی وتر ایجاد شده باز کرده،
روی یکی از نقاط ایجاد شده روی محیط دایره گذاشته و متوالیاً کمان می زنیم.
محاسبه طول یک کمان از دایره : برای محاسبه طول کمان از رابطه ی زیر استفاده می کنیم :

زاویه محاطی : زاویه ای است که رأس آن روی محیط دایره و دو ضلع آن وتر دایره باشد.
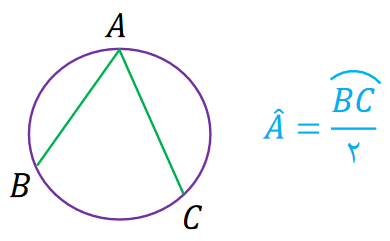
اندازه ی زاویه محاطی : زاویه محاطی برابر است با نصف اندازه ی کمان روبه رو آن.
نکته : زاویه های محاطی روبه رو به یک کمان برابرند.
نکته : اندازه ی زاویه ی محاطی ر وبه رو به قطر دایره ،90 درجه است.
مثال : اندازه ی کمان و زاویه خواسته شده را بنویسید.
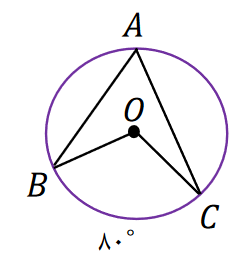
پاسخ تشریحی:

و حالا وقته تسته!!!




برای ارتباط با پشتیبان ویژه و اطلاع از شرایط مشاوره با رتبه هاي برتركانوني
به لينك زير مراجعه كنيد.


