
سلام به همه بچههای علاقمند به کامپیوتر و برنامهنویسی و هوش مصنوعی. همانطور که میدونین روز به روز دنیای هوش مصنوعی داره وسیعتر میشه و به حوزه مختلف از علوم راه یافته است. ما تصمیم داریم هر هفته با یک مقاله در این حوزه، شمارو با رویداد های دنیای هوش مصنوعی آشنا کنیم و مهمتر اینکه ریاضیات این حوزه رو با ساده سازی به شما دانش آموزان عزیز کانونی توضیح بدیم. در نهایت بتونیم قدم به قدم به کد نویسی در محیط پایتون برای مسئله های جذاب هوش مصنوعی برسیم. پیشنهاد میکنم هر هفته مارو با یک مقاله در این حوزه دنبال کنید.
شبکه عصبی پرسپترون – توابع فعال ساز
گفتیم که پرسپترون ساده ترین الگوریتم در شبکه های عصبی هست و یاد گرفتن ساختار پرسپترون، موجب میشه تا راحتتر به درک عمکلرد نورون ها و شبکه های عصبی برسیم. همچنین گفتیم که پرسپترون، الگوریتمی هست که ورودی رو تبدیل به یک خروجی باینری و یا دودویی میکرد. نورون موجود در شبکه پرسپترون، از دو بخش تشکیل شده. تابعی که ورودی ها رو با هم جمع میکنه ، و یک تابع فعال ساز. به نوعی میشه گفت که مهم ترین قسمت این نورون، همین تابع فعال ساز هست که میشه از توابع مختلف ریاضی برای تنظیم اون استفاده کرد. اما چرا توابع فعال ساز برای ما و شبکه های عصبی مهم هستند؟
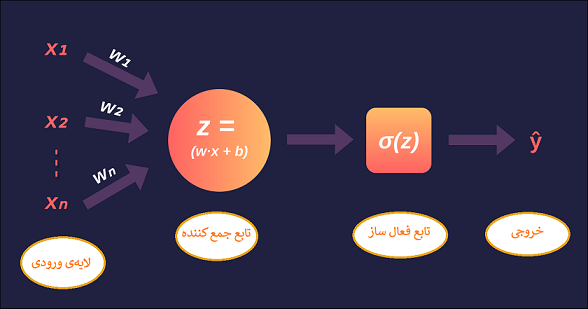
اگه خاطرتون باشه، در مقاله ای که در مورد عملکرد شبکه های عصبی داشتیم، گفتیم که نورونها رو مثل یه چراغ در نظر بگیرید که اگه روشن بشن، داده ها رو از خودشون عبور میدن و به لایه بعدی منتقل میکنند . در این شبیه سازی، توابع فعال ساز حکم کلید رو برای این چراغ فرضی ما داره، این توابع فعال ساز، توابع ریاضی مختلف هستند ؛ پس یه بار دیگه میبینیم که ریاضیات با دنیای هوش مصنوعی پیوند برقرار میکنه!
میدونیم که تابع در دنیای واقعی برای توصیف بسیاری از پدیدهها مورد استفاده قرار میگیره و بسیاری از پدیدههای طبیعی رو بهوسیله توابع ریاضی مدل سازی میشن . در مقاله قبلی، چند نمونه تابع فعال ساز رو براتون معرفی کردیم که در الگوریتم پرسپترون کاربرد داشت و در مثالی، تابع فعال ساز sign رو مرور کردیم. برای اینکه بهتر با عملکرد این توابع فعال ساز آشنا بشیم، و همچنین یه مروری هم به دنیای توابع ریاضی داشته باشیم، در این مقاله چند نمونه از مهم ترین توابع فعال ساز که هم در پرسپترون و به تبع اون در نورون های شبکه های عصبی کاربرد داره رو مرور میکنیم.
توابع فعال ساز step و یا پله ای
توابع پله ای ، همونطور که از اسمش پیداست، توابعی هست که نمودارش شبیه پله باشه! اما از لحاظ ریاضی ما به تابعی میگیم پله ای که این تابع توی قسمت های مختلف دامنه اش، مقدار ثابتی رو داشته باشه . برای مثال به شکل زیر دقت کنید :
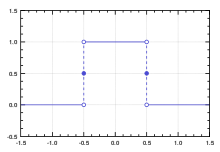
همونطور که میبینید، این تابع، در مقادیر کمتر از 0.5 – و بالاتر از 0.5 مقدارش صفر هست. اما برای ورودی هایی که مقدارشون بین 0.5 – تا 0.5 باشه، عدد ثابت یک رو اختصاص میده . اما این تابع، یه نکته دیگه ای هم داره ؛ و اونم اینه که اگه ورودی ما دقیقا برابر 0.5 – یا 0.5 باشه، مقدار 0.5 رو به عنوان خروجی به ما میده . اگه بخوایم این تابع رو به شکل ریاضی بیان کنیم، داریم :
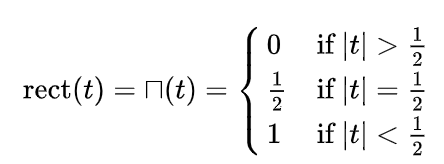
تابعی که در این مثال مورد بررسی قرار دادیم، تابع مستطیلی و یا Rectangular هست. تابع مستطیلی، یکی از توابع مهم پله ای به شمار میره. این تابع، با وجود شکل ساده ای که داره، در مباحث پیشرفته مخابراتی و پهنای باند کاربرد داره.
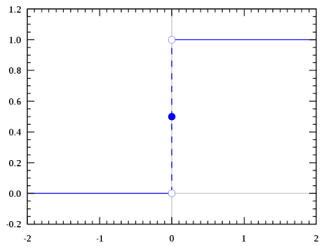
از توابع پله ای معروف دیگه ، تابع پله ای هوی ساید (Heaviside step function) و یا تابع پله ای یکه ای است. مقدار این تابع برای اعداد منفی، صفر و برای اعداد نامنفی، یک هست. همچنین زمانی که این تابع مقدار صفر رو به عنوان ورودی میگیره، به نوعی حد فعال سازیش به کار می افته و مقدار 0.5 رو به عنوان خروجی میده. البته میشه دامنه این تابع رو شیفت داد. یعنی طوری تنظیمش کرد که مثلا برای اعداد زیر 1 ، خروجی صفر بده و برای اعداد بالای صفر، خروجی 1 داشته باشه. این کار باعث میشه که حد فعال سازی رو جابهجا کنیم. پس در نورون های مختلف، حد فعال سازی رو با جابهجا کردن دامنه این تابع میشه تنظیم کرد.
توابع فعال ساز Sigmoid
تابع سیگموئید (Sigmoid function) یک تابع ریاضی است که شکلی مشابه با حرف S در زبان انگلیسی داره! این تابع، حقیقی، کراندار و مشتقپذیر و به ازای کلیه مقادیر حقیقی قابل تعریف بوده و دارای مشتق مثبتی هستش. رابطه کلی این دسته از توابع به شکل زیر هست :
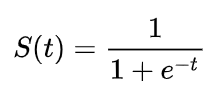
به طور کلی به توابعی که شکل آنها مشابه با حرف S هست، تابعهای سیگموئید یا دارای خمیدگی سیگموئید میگن. از جمله توابع سیگموئید میشه به تابع عملکرد لجستیک، تابع قطبی و منحنی ریچارد اشاره کرد. شکل زیر برخی از سیگموئید رو در کنار هم نشون میده. این توابع به گونه ای تنظیم شده اند که شیب اونا در مبدا مساوی یک باشه.
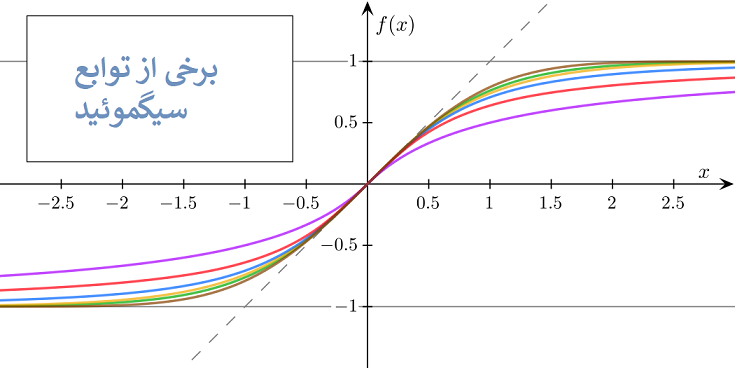
خروجی توابع بالا در بازه منفی 1 تا مثبت یک می باشد و برای مقادیر مثبت بینهایت و منفی بینهایت، مقدار 1 و 1- رو میده . اما نوعی از توابع سیگموئید وجود داره که به ازای دامنه حقیقی، f(x) اش در بازه صفر تا یک هست . این تابع، لجستیک سیگموئید نام داره که فرم کلی و استانداردش رو در شکل زیر میتونید ببینید:
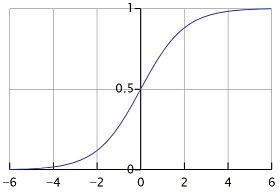
این تابع هم یک ورودی منفی بینهایت تا مثبت بینهایت را به یک بازهی ۰ تا ۱ تبدیل میکنه. اما همانطور که مشاهده میکنید دیگه این کار به صورت خطی انجام نمیده. برای مثال اگر عدد ۰ به تابع لجستیک سیگموئید داده بشه، خروجی برابر ۰.۵ خواهد بود. به این مدل توابع، توابع فعالساز غیر خطی (non-linear) گفته میشه. استفاده از این توابع میتونه ترکیبها و ویژگیهای پیچیدهتری رو از شبکههای عصبی کسب کنه و خاصیت غیر خطی بودن اون، شبکه رو قادر به شناسایی الگوهایی به مراتب پیچیدهتر میکنه.
تابع فعال ساز ReLU
این تابع از پرکاربردترین توابع در شبکه های عصبی عمیق هستش و از سال 2018 به بعد، محبوبترین تابع فعال سازی شناخته میشه. به طوری که امروزه در بینایی کامپیوتر، پردازش متن، تشخیص صوت و شبکههای عصبی عمیق به جای توابع فعال سازی لجستیک از تابع ReLU استفاده میشه. فرمول ریاضی این تابع به صورت زیر هست :
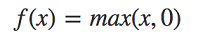
در صورتیکه ورودی کمتر از ۰ باشد، تابع فعالسازی ReLU صفر (۰) و در غیر اینصورت مقدار خام را خروجی میدهد. به عبارت دیگر، اگر مقدار ورودی بیشتر از ۰ باشد، تابع ReLU همان مقدار ورودی را خروجی میدهد. نمودار این تابع به صورت زیر هست :
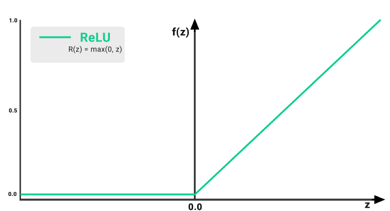
پس این تابع دیگه صرفا مثل پرسپترون خروجی باینری تولید نمیکنه و در الگوریتم های متنوع دیگه شبکه های عصبی کاربرد داره که به تدریج با اونها هم آشنا خواهیم شد.
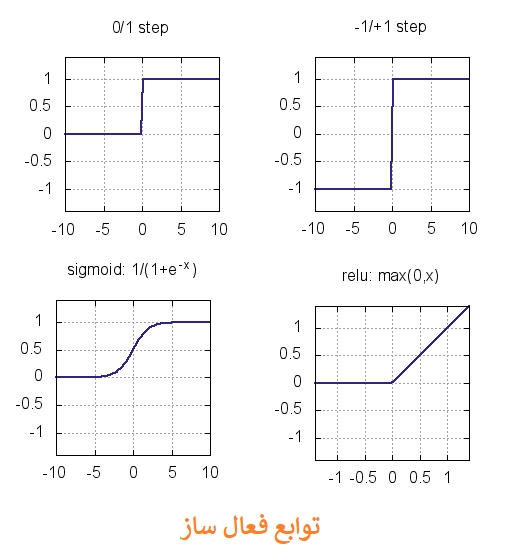
پس در این مقاله با چند نوع از توابع فعال ساز آشنا شدیم که در شکل زیر میتونید همش رو یکجا ببنید، هر چند تنوع زیادی در این توابع وجود داره و دنیای جذاب ریاضیات و توابع، باعث شده که فناوری هوش مصنوعی و شبکه های عصبی روز به روز با پیشرفت های بزرگی همراه بشه. پس با ما در ادامه سفرمون به دنیای جذاب هوش مصنوعی همراه باشید ...
- منابع
https://www.simplilearn.com/tutorials/deep-learning-tutorial/perceptron
https://en.wikipedia.org/wiki/Rectangular_function
https://www.aparat.com/v/wI5nh/
https://wikipredia.net/fa/Sigmoid_function
https://chistio.ir/
https://virgool.io/@alifallahi/
https://hooshio.com/توابع-فعال-سازی/
کلیدواژه ها
دوستان عزیزم؛ برای ارتباط با برترها و رزرو پشتیبان ویژه پیج کانون برترها را دنبال کنید.
همچنین میتوانید با شماره 0218451 داخلی 3123 تماس بگیرید.



