سلام
در این مطلب میخواهیم به جمع بندی مبحث انواع تابع بپردازیم.
همچنین سوال یا پیشنهاد خودتون رو در قسمت کامنت های این مطلب مطرح کنید.
با ما همراه باشید!
 | مهدیه امین فارغ التحصیل رشته مهندسی شیمی دانشگاه شریف رتبه 108 منطقه سه- کنکور ریاضی 1394 |
برای یادآوری مطالب مربوط به مبحث تابع ریاضی دهم میتوانید به لینک زیر مراجعه کنید.
تابع- ریاضی دهم- درسنامه - مهدیه امین
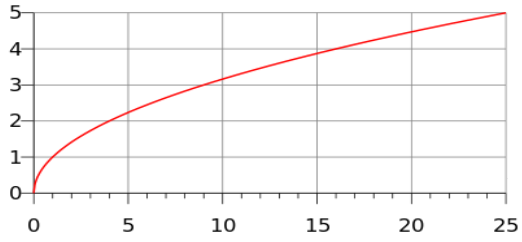
توابع گویا (کسری)

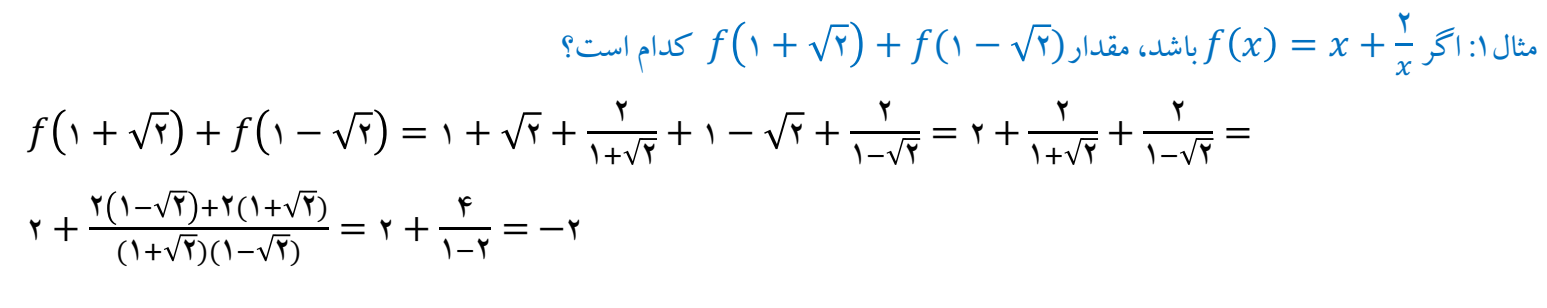
توابع رادیکالی (تابع ریشه دوم)
با توجه به نمودار تابع y=√x، دامنه و برد این تابع اعداد حقیقی نامنفی است.
دامنه توابع رادیکالی: برای محاسبه دامنه این توابع باید عبارت زیر رادیکال (زوج) را بزرگتر از مساوی صفر قرار دهیم و نامعادله را حل کنیم.

توابع پلهای و تابع جزء صحیح
تابع پلهای: هر تابعی که بتوان دامنه آن را به تعدادی بازه تقسیم بندی کرد به طوری که تابع روی هر کدام از این بازهها تابع ثابت باشد، یک تابع پلهای میباشد.
جزء صحیح: برای هر عدد حقیقی مانند x، جزء صحیح آن بزرگترین عدد صحیحی است که از x بیشتر نباشد. جزء صحیح x را با نماد [x]نمایش میدهیم. برای مثال [3.2 ]=3
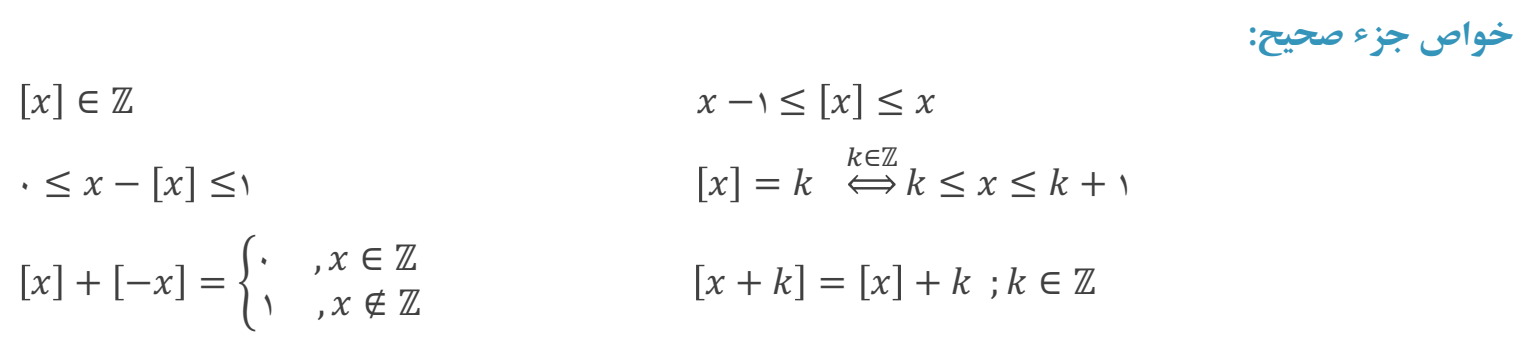
تابع جزءصحیح: گونه خاصی از توابع پلهای که به هر عدد حقیقی، جزء صحیح آن عدد را نسبت میدهد، تابع جزء صحیح نامیده میشود و آن را به صورت f(x)=[x]نمایش میدهند. دامنه تابع جزءصحیح، مجموعه اعداد حقیقی و برد آن مجموعه اعداد صحیح است.
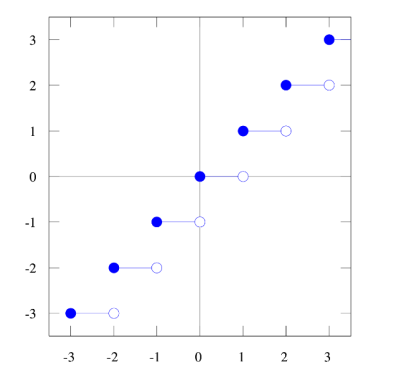
نمودار دو تابع مهم:
نمودار تابع y=x-[x]
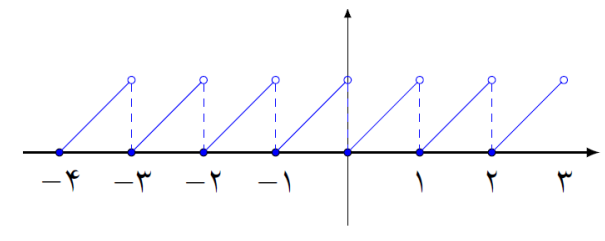
نمودار تابع y=[x]+[-x]
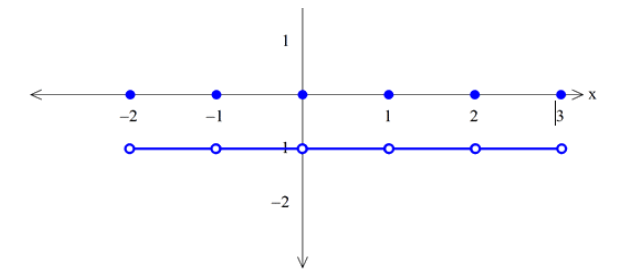
برد تابع
برد تابع، محدوده تغییرات y یا بزرگترین مجموعهای است که به ازای تمام مقادیر دامنه تابع برای y به وجود میآید.
محاسبه برد توابع:
1. اگر تابع به صورت مجموعهای از زوجهای مرتب بیان شود، مجموعهی مولفههای دوم آن، برد تابع را تشکیل میدهند.
2. برد توابع چند جملهای درجه فرد، مجموعه اعداد حقی است.
3. در توابع درجه دوم، برای یافتن برد، از مربع کامل کردن میتوان استفاده کرد.
4. برای یافتن برد توابع چند ضابطهای، برد هر تابع را در دامنه داده شده به دست میآوریم و سپس بین بردها به دست آمده اجتماع میگیریم.
5. در توابع کسری که صورت و مخرج ساده میشوند، برای یافتن برد، ابتدا آن را ساده میکنیم. سپس مقدار تابع به دست آمده را به ازای ریشههای مخرج از برد حذف میکنیم.
تساوی دو تابع
دو تابع f و g را مساوی میگویند، هرگاه:
1. دامنه آنها با هم برابر باشند.
2. به ازای هر عضو از دامنه یکسان، مقادیر به دست آمده توسط دو تابع f و g با هم برابر باشند، در واقع داشته باشیم:
x∈D :f(x)=g(x)



پاسخ تست ها رو میتونید در pdf بارگذاری شده در انتهای مطلب مشاهده کنید.
دوستان عزیزم؛ برای ارتباط با رتبه برترها صفحه اینستاگرام زیر رو دنبال کنید.


