تابع_ریاضی دهم_محمدامین شیخی

روابط مهم در حل سوالات سهمی- مبحث تابع- ریاضی دهم- محمدامین شیخی

سلام، محمدامین شیخی هستم، رتبه 15 منطقه2 کنکور ریاضی 1400 با میانگین درصد ریاضی 88 در آزمون های کانون و دانشجوي مهندسي مکانيک دانشگاه صنعتي شريف. از آنجايي که يکي از مباحث مهم رياضي دهم مبحث تابع است، در این مطلب قصد داریم نکات و تکنیک های مهم در حل سوالات مربوط به سهمی در ریاضی دهم را بررسی کنیم و با حل چند تست، کاربرد این نکات را بهتر درک کنیم.

*نمودار توابعی به فرم f(x)=ax2+bx+c (a≠0) که به صورت چند جمله ای درجه دوم هستند، سهمی نام دارد و جهت دهانه ی سهمی، به علامت a بستگی دارد:

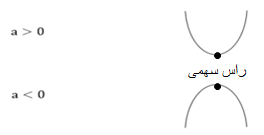
*عرض از مبدأ(عرض نقطۀ برخورد با محور y) برای سهمی به ضابطۀ f(x)=ax2+bx+c، برابر با c می باشد.

*نقاط برخورد سهمی با محور x، همان ریشه های معادله ی ax2+bx+c=0 هستند که از این رابطه بدست می آیند:

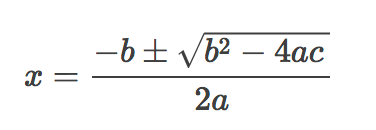
*عبارت b2-4ac را برای اختصار با ∆ نمایش می دهیم و روابط زیر برای ∆ برقرار هستند:

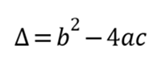
0<∆    سهمی در 2 نقطه به طول های   محور  x را قطع ميکند.

0=∆   سهمی در 1 نقطه به طول   منفيb  تقسيم بر  2a محور x را قطع می کند(راس سهمی بر محور x مماس است).   

0>∆   سهمی محور x را قطع نمی کند.

طول و عرض رأس سهمی را به ترتیب با xo و yo نمایش می دهیم که از روابط زیر محاسبه می شوند:  

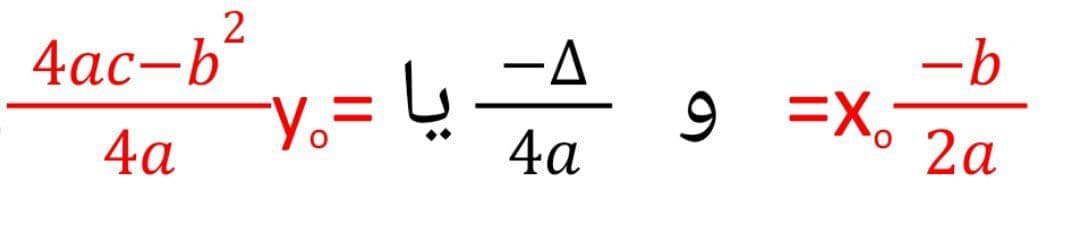
*خط x=xo، محور تقارن سهمی نام دارد.

 در برخی از سوالات سهمی که در آنها اطلاعات خوبی دربارۀ مختصات رأس سهمی داریم، می توانیم ضابطه ی سهمی را به صورت :

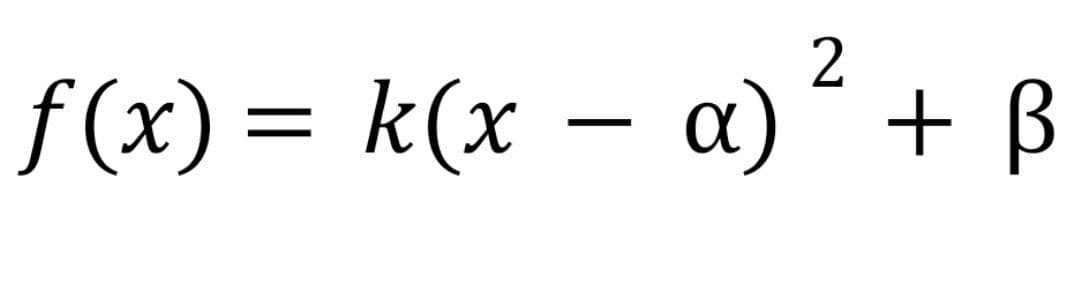
در نظر بگیریم بطوریکه  a و  B به ترتیب طول و عرض رأس سهمی می باشند و برای k داریم:

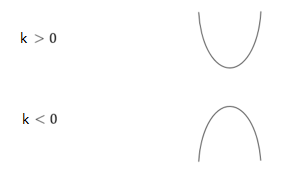
*اگر خط افقی y=m سهمی به ضابطه ی f(x)=ax2+bx+c را در دو نقطه به طول های x1 و x2 قطع کند، همواره رابطه ی:

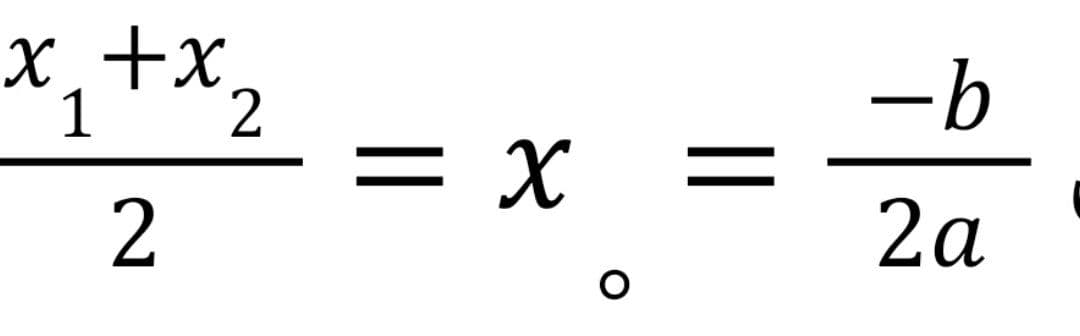
برقرار است.(به عبارت دیگر، طول رأس سهمی برابر با میانگین طول آن دو نقطه است)

 فايل کامل درسنامه و تست و پاسخ مبحث تابع رياضي دهم را ميتوانيد از قسمت زير دانلود کنيد.

محمدامين شيخي - رتبه 15 منطقه 2- مهندسي مکانيک دانشگاه صنعتي شريف