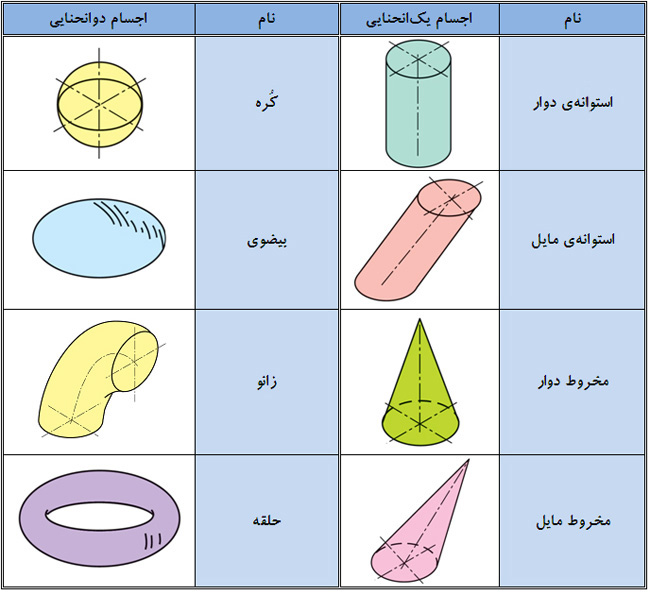
دستهی بزرگی از اجسام، دارای سطوحی غیرتخت یا منحنی هستند؛ مانند استوانه، مخروط و كره. در جدول زیر، تعدادی از این اجسام، معرفی شدهاند.
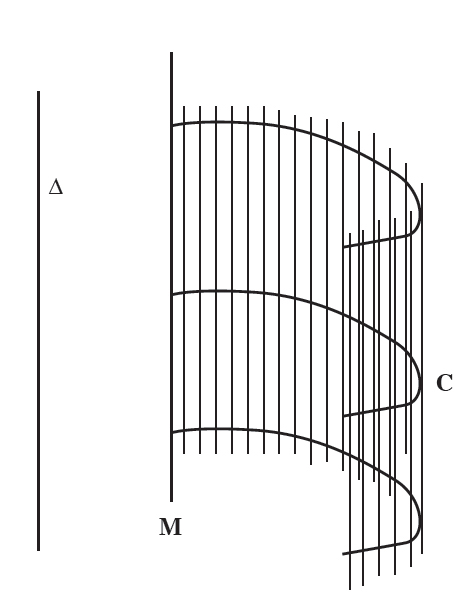
اگر خط راست M
به گونهای در فضا تغییر مكان دهد كه همواره بر منحنی ثابت C متكی بوده و با خط
ثابتی موازی باشد، سطحی به وجود میآید كه آن را سطح استوانهای مینامند. قسمت محدودی از این سطح را استوانه میگویند.
خط M را مولد و منحنی C را راهنما یا هادی میگویند.
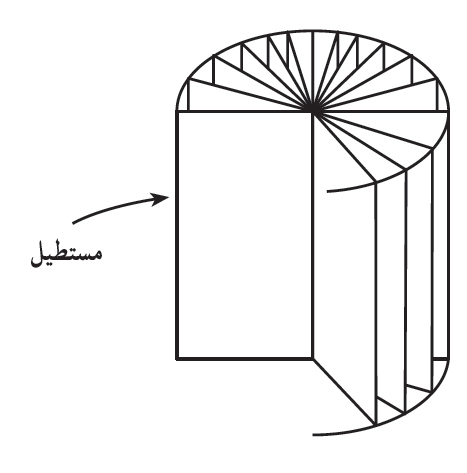
اگر مولدها بر منحنی C (قاعدهی استوانه) عمود باشند، استوانه را استوانهی قائم و در غیراینصورت آن را استوانهی مایل مینامند. استوانهی قائمی كه قاعدهی آن به شكل دایره باشد، استوانهی دوار نامیده میشود.
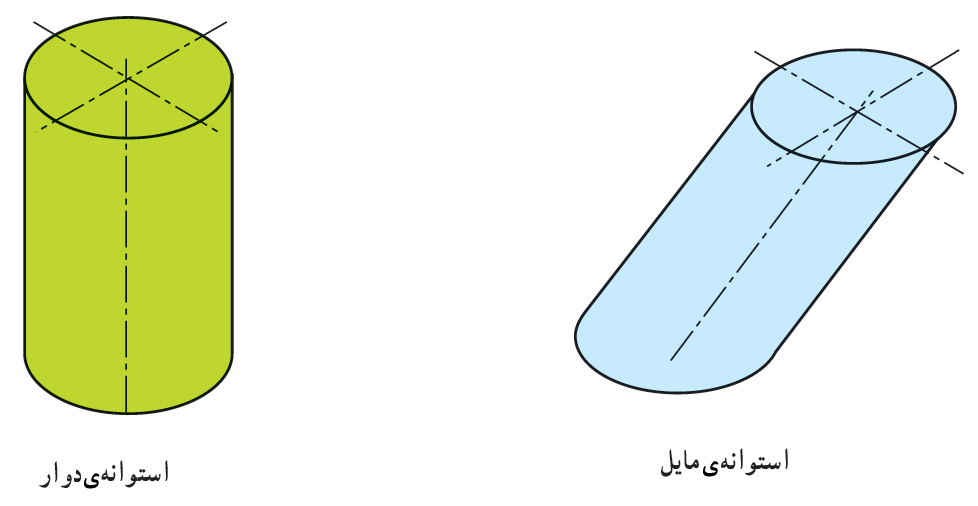
استوانهی دوار در حقیقت از چرخش یك مستطیل به دور یكی از اضلاع آن ساخته میشود.
مخروط
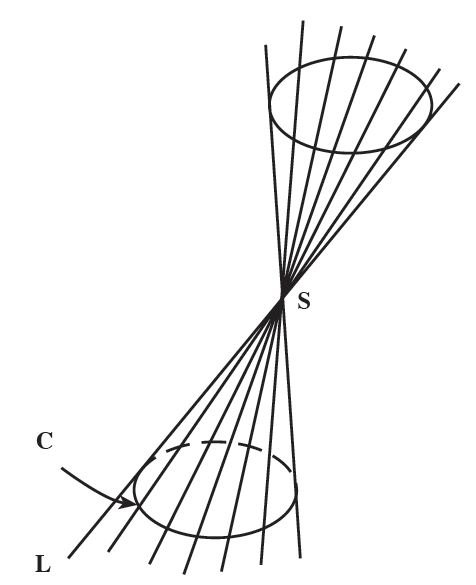
اگر خطی مانند L به گونهای در فضا حركت كند كه همواره از نقطهی ثابتی مانند S بگذرد و بر یك منحنی ثابت مانند C متكی باشد، سطح مخروطی ساخته میشود. خط L را مولد و منحنی C را راهنما مینامند.
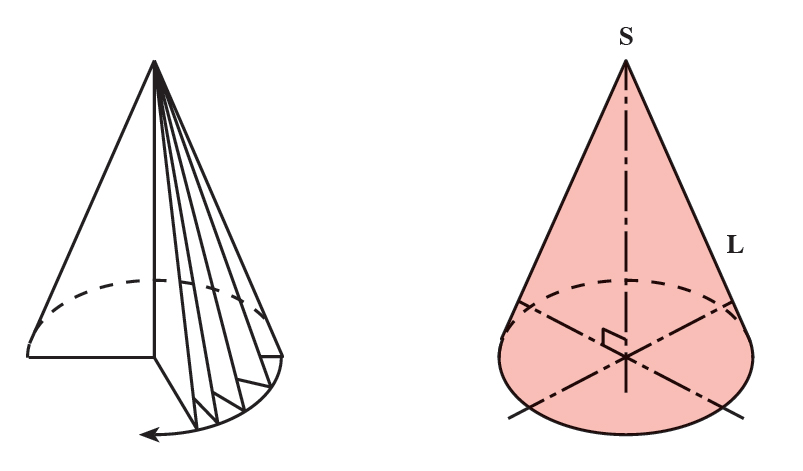
مخروط نیز مانند استوانه میتواند قائم یا مایل باشد. در مخروط قائم، محور مخروط بر مركز قاعده عمود است. مخروط قائمی كه قاعدهی آن به شكل دایره باشد، مخروط دوار نامیده میشود. مخروط دوار میتواند از چرخش یك مثلث قائمالزاویه (راستگوشه) به دور یكی از اضلاع زاویهی قائمه ساخته شود.
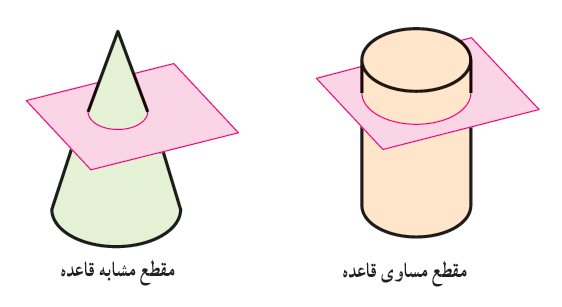
استوانه و مخروط، از اجسام یكانحنایی به شمار میروند. اگر این اجسام را با یك صفحه به موازات قاعده برش دهیم، مقطع حاصل، شكلی مشابه یا برابر با قاعده خواهد بود.
كُره
كُره از اجسام دوانحنایی است. اگر یك دایره یا نیمدایره به دور قطر خود بچرخد، حجم كُره ساخته میشود.
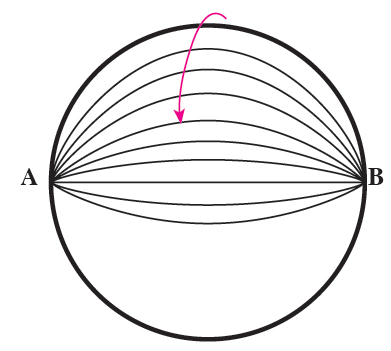
بخشهای گوناگون كره (قاچ، عرقچين، منطقه و نيمكره)، در شكل زیر معرفی شدهاند.
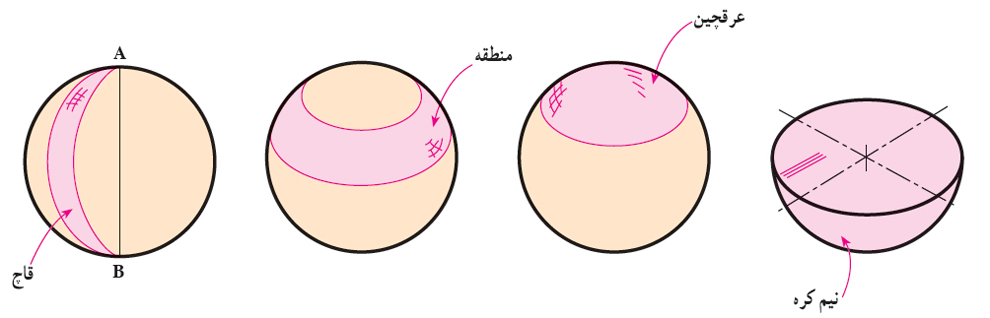
بیضوی و شلجمی
از چرخش یك بیضی به دور قطر بزرگ خود، حجمی پدید میآید كه بیضوی نام دارد.
اگر بیضی به دور قطر كوچك خود بچرخد، حجمی به شكل عدس به وجود میآید كه آن را شلجمی مینامند.
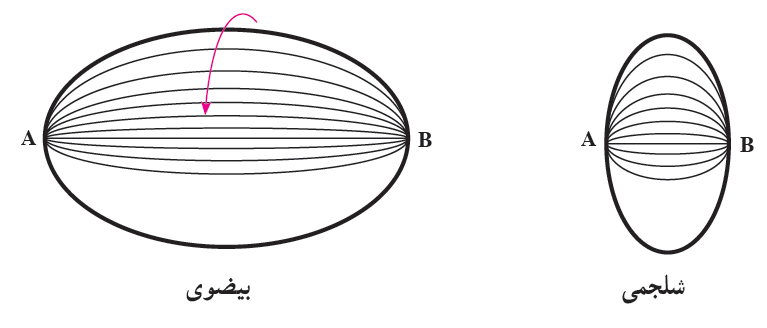
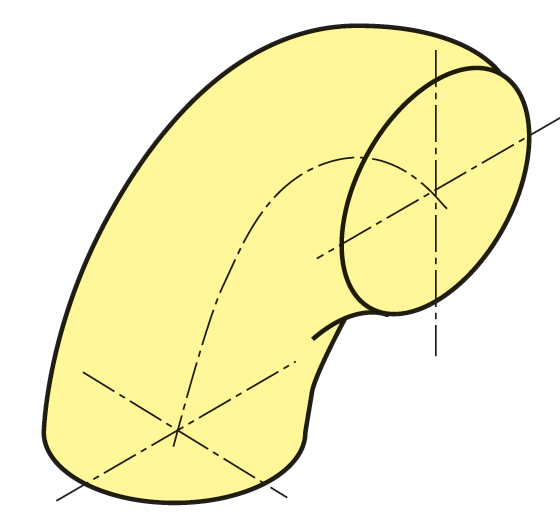
حلقه و زانو
اگر دایرهی C، چنان دوران كند كه مركز آن همیشه متكی بر یك دایرهی دیگر به نام 'C بوده و سطح آن نیز عمود بر 'C باشد، حجمی پدید میآید كه آن را حلقه مینامیم. این حجم، در حقیقت استوانهای است كه آن را به شكل حلقه درآورده باشند.
بخشی از حلقه، (مانند یكچهارم آن) را، زانو مینامند.