حد و پیوستگی- بخش سوم-درسنامه- سروش اسماعیلی

دانش آموزان عزیز سلام 

در این سری مطالب میخواهیم در چندبخش، مبحث حد و پیوستگی را به طور کامل پوشش دهیم .

امیدوارم که این مطالب برای شما مفید باشد.

🟣ویژگی های مطلب🟣 

1- درسنامه کامل به همراه مثال و نکات‌ حد و پیوستگی

2- 5 تست شناسنامه دار از این مبحث

3-پاسخ کلیدی تست ها در انتهای مطلب

4- ویدئو  و تدریس پاسخ تشریحی تست ها

مولف: سروش اسماعیلی  رتبه 395 کنکور ریاضی 1402 دانشجوی مهندسی مکانیک دانشگاه تهران

در ابتدا سوالات مهمی که از این بخش در امتحانات نهایی 1403  آمده است را مرور میکنیم تا اهمیت مبحث درک شود.

سوالات حد و پیوستگی یازدهم خرداد 1404

پیوستگی در نقطه

از معنای خود کلمه میتوان دریافت که تابع در آن نقطه دارای قطع شدگی نباشد. یعنی بتوان بدون برداشتن قلم از روی کاغذ نمودار تابع را بتوان رسم کرد. به طور ریاضی شرط پیوستگی تابع در یک نقطه را به طور زیر تعریف میکنیم:

تابع در آن نقطه حد داشته باشد و حد تابع با مقدار تابع در آن نقطه برابر باشد

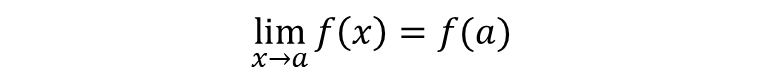
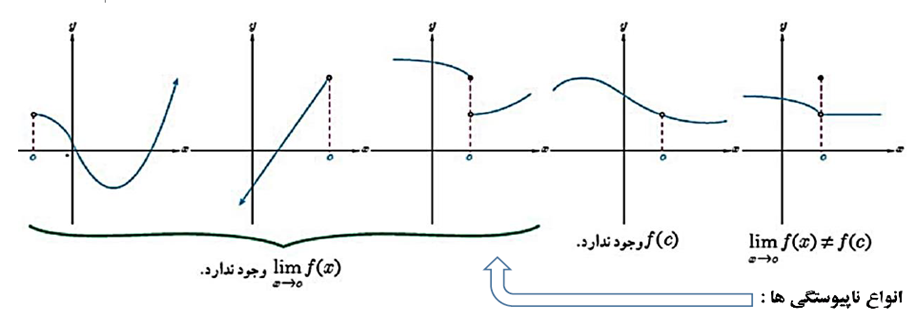
با توجه به تعریف توابع زیر ناپیوسته هستند

پیوستگی چپ: تابع در نقطه x=a پیوستگی چپ دارد هرگاه

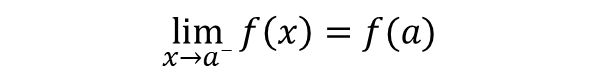
پیوستگی راست: تابع در نقطه x=a پیوستگی راست دارد هرگاه

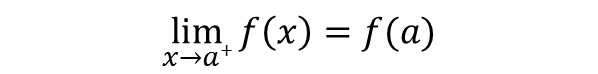
تابع f در نقطه x=a پیوسته است اگر و تنها اگر f در a هم از راست و هم از چپ پیوسته باشد.

پیوستگی در بازه

نکات مهم پیوستگی

(1توابع چند جمله‌ای روی R پیوسته‌اند.  2)توابع کسری گویا در ریشه های مخرج ناپیوسته اند.

3) توابع  sinx ,cosxروی R پیوسته‌اند

4) اگر f روی R پیوسته باشد انگاه:

•توابع fn, |f|, √(2n+1&f)  نیز روی R پیوسته اند.

•تابع  logfروی بازه هایی که  f>0و تابع √(2n&f) روی بازه های که f≥0 پیوسته است.

5) اگر توابع f, و g در یک نقطه پیوسته باشند انگاه توابع f±g, f.g, cf, f/g (g≠0) نیز در آن نقطه پیوسته هستند.

6) اگر تابع g در نقطه x=a و تابع f در نقطه g(a) پیوسته باشند انگاه تابع fog در نقطه a پیوسته است.

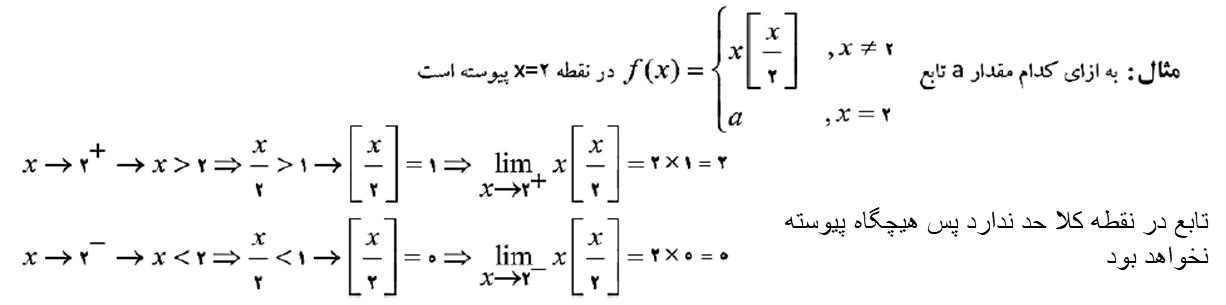
پیوستگی توابع شامل جزء صحیح

اگر تابع f(x) در x=a پیوسته و غیر صحیح باشدباشد آنگاه تابع [f(x)] نیز در این نقطه پیوسته خواهد بود. اگر صحیح باشد تابع [f(x)] پیوسته نخواهد بود مگر اینکه x=a طول نقطه مینیمم نسبی تابع باشد. به طور مثال در تابع x2 مشاهده میشود که هنگام براکت گیری نقاط صحیح دیگر پیوسته نیستند به جز نقطه x=0 که مینیمم نسبی است.

در صورتی که f در x=a پیوسته و صحیح باشد:

1)اگر f صعودی اکید باشد تابع [f(x)] پیوستگی راست دارد.

2)اگر f نزولی اکید باشد تابع [f(x)] پیوستگی چپ دارد.

مثال) تابع f(x)=[x] بر بازه (3,n) پیوسته است. حداکثر مقدار n چقدر است؟

اگر n>4 باشد انگاه مقدار تابع در x=4 ناپیوسته میشود پس n≤4 است و تابه در بازه (3,4) پیوسته میشود.(توجه کنیم انتهای دو سمت بازه، بسته نیست و باز است پس n برابر خود 4 میتواند باشد)

مثال) تابع f(x)=(x2-1)[(x+1)/2] روی بازه (-5,3) در چند نقطه ناپیوسته است؟

اگر f(x) و g(x) در x=a پیوسته باشند اما [g(x)] پیوسته نباشد؛ به شرطی که f(a)=0 باشد میتوان گفت تابع f(x)[g(x)] در x=a پیوسته است.

تابع براکت دربازه مشخص شده در سه نقطه x=1,x=-1 , x=-3 داخلش صحیح میشود که کاندید ناپیوستگی میتوانند باشند.

(x+1)/2=k⇒x=2k-1 (k∈Z)⇒x=1,x=-1,x=-3

 اما طبق نکته بالا در نقاط 1,-1 که ضرایب صفر کننده هستند پیوسته است. پس فقط x=-3 نقطه ناپیوستگی است.

🔵برای مطالعه ادامه درسنامه و سوالات کنکور این مبحث، لطفا جزوه را از فایل ضمیمه دانلود کنید 🔵

🔵عضویت در کانال تلگرام کانون برترها🔵