حد و پیوستگی- بخش دوم-درسنامه- سروش اسماعیلی

دانش آموزان عزیز سلام 

در این سری مطالب میخواهیم در چندبخش، مبحث حد و پیوستگی  را به طور کامل پوشش دهیم .

امیدوارم که این مطالب برای شما مفید باشد.

🟣ویژگی های مطلب🟣 

1- درسنامه کامل به همراه مثال و نکات‌ حد و پیوستگی

2- 5 تست شناسنامه دار از این مبحث

3-پاسخ کلیدی تست ها در انتهای مطلب

4- ویدئو  و تدریس پاسخ تشریحی تست ها

مولف: سروش اسماعیلی  رتبه 395 کنکور ریاضی 1402 دانشجوی مهندسی مکانیک دانشگاه تهران

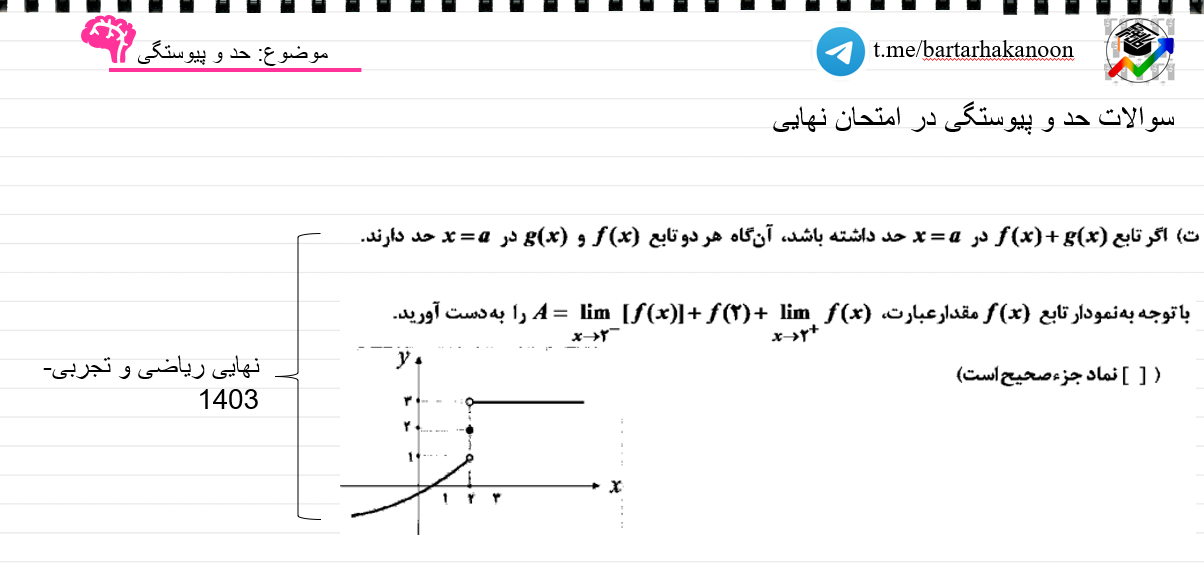
در ابتدا سوالات مهمی که از این بخش در امتحانات نهایی  1403  آمده است را مرور میکنیم تا اهمیت مبحث درک شود.

سوالات حد و پیوستگی یازدهم خرداد 1404

حد توابع براکتی

در محاسبه حد این توابع، مقدار عددی براکت را محاسبه و جایگذاری میکنیم و ادامه فرایند حد گیری را انجام میدهیم. به نوعی بخش براکتی را از بین برده و با یک عدد جایگذاری میکنیم. از انجا که در براکت مهم هست که مقدار عددی از کدام سمت نزدیک میشود(مانند حدود چپ و راست)، یکی از حالت های زیر به وجود می‌اید.

اگر در یک همسایگی a تابع f(x) با مقادیر بیشتر یا کمتر  از L به L نزدیک شود به ترتیب داریم:

تابع در نقاطی که مقدار درون براکت صحیح میشود حد ندارد مگر اینکه آن نقطه ماکسیمم یا مینیمم نسبی باشد!  

زیرا حد راست آنها برابر L و حد چپ برابر L-1 میشود. 

مثال) اگر باشد مقدار  f(x)=[x]+[-2x]حد  lim┬(x→1)⁡f(x) را در صورت وجود بیابید.

حد چپ و راست را محاسبه کرده و اگر برابر باشند تابع حد دارد:

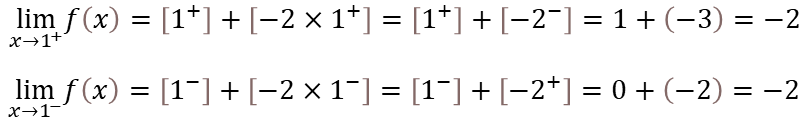
در توابع به شکل زیر برای محاسبه حد در هر نقطه صحیح و غیر صحیح از ضابطه g(x) استفاده میکنیم زیرا مفهوم حد گیری در نقطه به معنای نزدیک شدن ازهمسایگی آن نقطه است که اگر حتی خود نقطه صحیح باشد در همسایگی آن اعداد غیرصحیح وجود دارند.

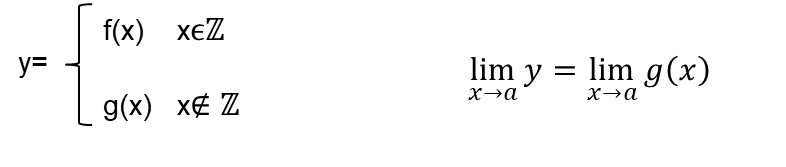
رفع ابهام

در محاسبه حد در جایگذاری مقادیر به عبارات زیر برخوردیم یعنی حالت مبهم هست و توانایی محاسبه حد با روش های قبل را نداریم. پس ابتدا باید حد را رفع ابهام کرده و سپس از روش های گذشته استفاده کنیم. حالت های مختلف ابهام به شرح زیر است که ما تنها حالت 0/0 را بررسی میکنیم.

روش اول) حذف عامل صفر کننده

در این روش عامل صفر کننده را که هم در صورت و هم در مخرج وجود دارد از صورت و مخرج باهم ساده میکنیم. برای اینکار میتوان از اتحاد ها و تجزیه استفاده کرد. اگر عبارت مخرج گنگ باشد ابتدا انرا گویا کرده و سپس عامل صفر کننده را حذف میکنیم.

اگر عبارت قدرمطلق داشتیم ابتدا علامت داخل آنرا با جایگذاری عدد مشخص کرده و سپس خود عبارت یا قرینه داخل قدرمطلق را طبق علامت جاگذاری میکنیم تا علامت قدرمطلق حذف شود.

اگر عبارت براکت داشتیم ابتدا مقدار عددی آنرا محاسبه و جاگذاری میکنیم تا عبارت براکت حذف شود

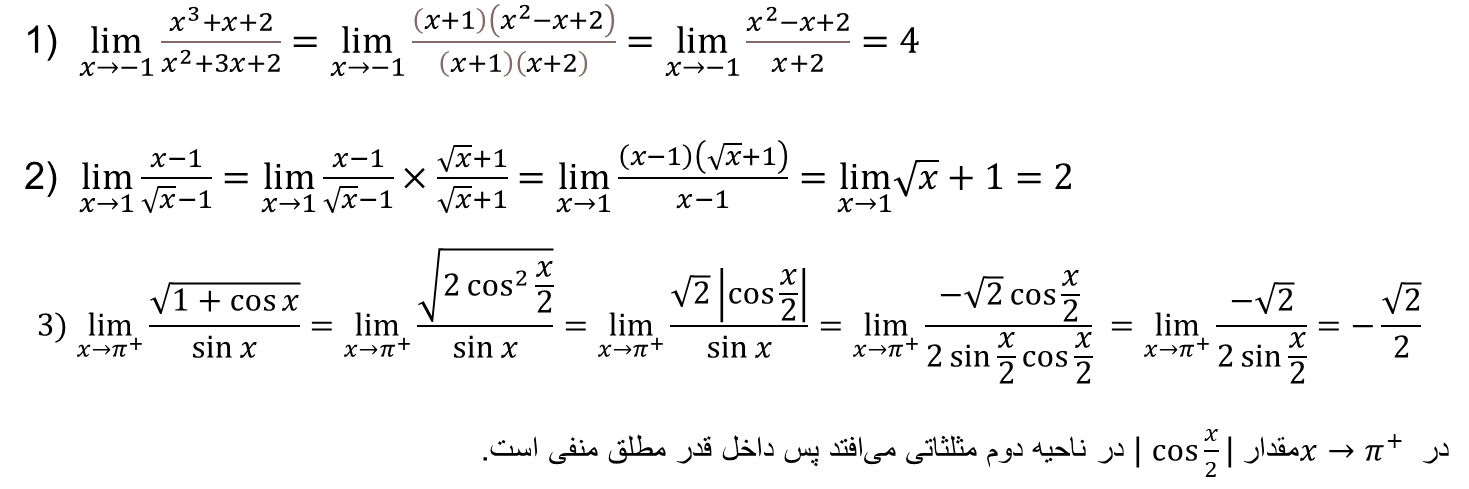
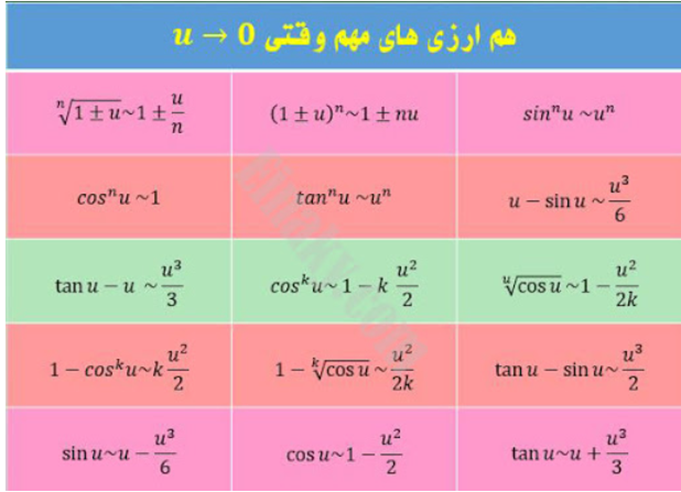
روش دوم) هم‌ارزی

در این روش به جای برخی توابع عبارت های متناظر با آنها را قرار میدهیم و به نوعی شکل حد تغییر پیدا میکند اما پاسخ آن با حالت قبل یکسان است.

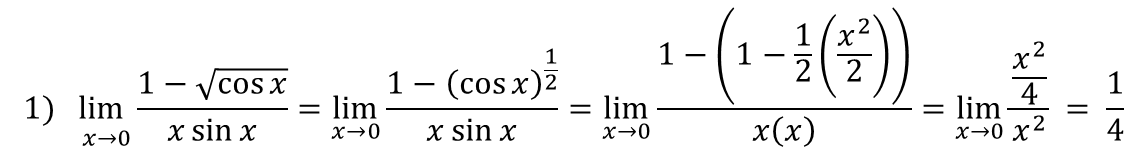
روش سوم) هوپیتال (پس از یادگیری مبحث مشتق این مطلب را بخوانید)

در این روش از عبارت صورت و مخرج هر کدام جداگانه مشتق گرفته میشود و از توابع جدید حاصل از مشتق حد گرفته میشود. اثبات میشود که حاصل این حد جدید با حد تابع قبل تفاوتی ندارد.

lim┬(x→a)  f(x)/((x) )=lim┬(x→a)   (f^′ (x))/(g^′ (x) )=L

اگر با یک مرحله هوپیتال گیری همچنان حد مبهم بود باز هم هوپیتال میزنیم.

در موارد مهیا بودن هم‌ارزی بهتر است ابتدا هم‌ارزی گرفته شود و اگر کسر همچنان مبهم بود هوپیتال میگیریم.(در کل هم ارزی اولویت دارد)

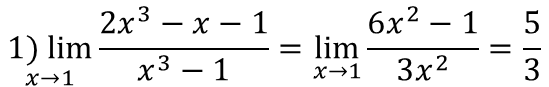
🔵برای مطالعه ادامه درسنامه و سوالات کنکور این مبحث، لطفا جزوه را از فایل ضمیمه دانلود کنید 🔵

🔵عضویت در کانال تلگرام کانون برترها🔵