حد و پیوستگی- بخش اول-درسنامه- سروش اسماعیلی

دانش آموزان عزیز سلام 

در این سری مطالب میخواهیم در چندبخش، مبحث حد و پیوستگی  را به طور کامل پوشش دهیم .

امیدوارم که این مطالب برای شما مفید باشد.

🟣ویژگی های مطلب🟣 

1- درسنامه کامل به همراه مثال و نکات‌ حد و پیوستگی

2- 5 تست شناسنامه دار از این مبحث

3-پاسخ کلیدی تست ها در انتهای مطلب

4- ویدئو  و تدریس پاسخ تشریحی تست ها

مولف: سروش اسماعیلی  رتبه 395 کنکور ریاضی 1402 دانشجوی مهندسی مکانیک دانشگاه تهران

در ابتدا سوالات مهمی که از این بخش در امتحانات نهایی 1402 و 1403  آمده است را مرور میکنیم تا اهمیت مبحث درک شود.

سوالات حد و پیوستگی یازدهم خرداد 1404

حال به سراغ درسنامه حد  میرویم

اگر x یک عدد حقیقی باشد، هر بازه مانند (a,b) که شامل x باشد را یک همسایگی x مینامیم. اگر x را از این بازه حذف کنیم به بازه (a,b)-{x} میرسیم که آن را همسایگی محذوف x مینامیم.

بازه همسایگی محذوف را به صورت  (a,x)∪(x,b) نیز نشان میدهیم.

همسایگی چپ و راست: اگر k>0 باشد، بازه (x,x+k) را   یک همسایگی راست و بازه (x-k,x) را یک همسایگی چپ  x مینامیم.

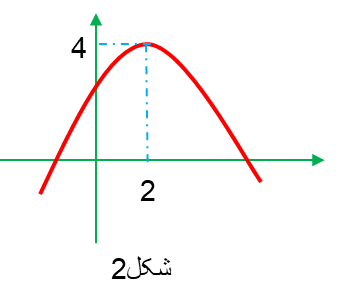
حد از مفاهیمی است که برای تحلیل و بررسی رفتار یک تابع استفاده میشود. حد به ما کمک میکند تا متوجه شویم با تغییر مقادیر ورودی یک تابع خروجی های آن چگونه تغییر میکنند. به طور مثال به شکل شماره 1 توجه کنید. در این نمودار خطی هر چه ورودی های تابع به عدد 1 نزدیک تر میشوند خروجی ها نیز به مقدار 3 میل میکنند.

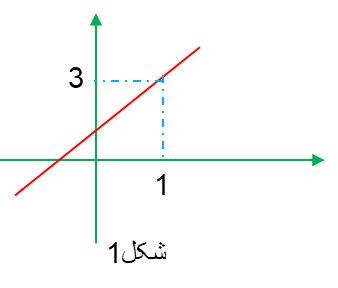
و یا در شکل 2 زمانی که به عدد 2 نزدیک میشویم خروجی ها به مقدار 4 نزدیک میشوند تا به خود عدد 2 برسیم که خروجی آن خود عدد 4 است.

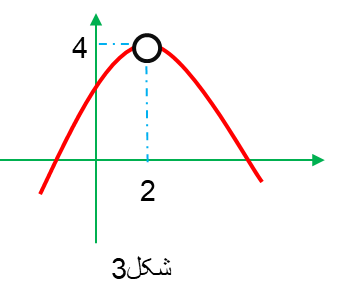
ممکن است یک تابع در نقطه a تعریف نشده باشد اما آن نقطه دارای حد است( به شکل 3 توجه کنید)

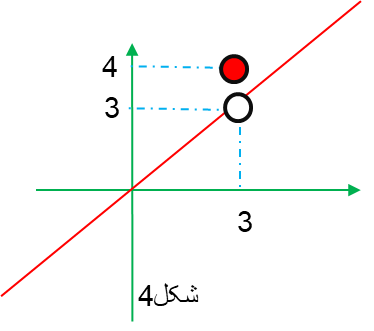
و حتی ممکن است یک تابع در نقطه a مقدار داشته و دارای حد نیز باشد اما مقدار حد با مقدار تابع متفاوت باشد. در شکل 4 مقدار تابع در نقطه 3 برابر 4 است اما مقدار حد در این نقطه برابر 3 است. به اصطلاح در این نقطه تابع پرش داشته است.

تعریف حد

اگر تابع f در یک همسایگی a (به جز احتمالا خود a) تعریف شده باشد، میگوییم تابع f زمانی که به عدد a نزدیک میشویم برابر عدد حقیقی L است هرگاه بتوان مقادیر تابع f به اندازه هر مقدار دلخواهی به عدد L نزدیک کرد مشروط به آن که متغیر x تابع از هر دو سمت چپ و راست به قدر کافی به a نزدیک شود. در این صورت میتوان نوشت:

lim┬(x→a)⁡〖f(x)=L〗

شرط لازم حد داشتن تابع f در نقطه a این است که تابع در هر دو همسایگی چپ و راست a تعریف شده باشد پس میتوان گفت توابع در نقاط ابتدا و انتهای دامنه حد ندارند.

تعریف دقیق و اثبات حد با روش اپسیلون دلتا است که در کتاب درسی اشاره‌ای نشده است.

حدهای یک طرفه

حد راست: اگر تابع f در یک همسایگی راست a تعریف شده باشد، حد راست تابع در نقطه a برابر L است هرگاه مقادیر تابع f به اندازه هر مقدار دلخواهی به عدد L نزدیک کرد مشروط به آن که متغیر x تابع از سمت راست به قدر کافی به a نزدیک شود. در این صورت مینویسیم:

lim┬(x→a+)⁡〖f(x)=L〗

حد چپ:اگر تابع f در یک همسایگی چپ a تعریف شده باشد، حد چپ تابع در نقطه a برابر L است هرگاه مقادیر تابع f به اندازه هر مقدار دلخواهی به عدد L نزدیک کرد مشروط به آن که متغیر x تابع از سمت چپ به قدر کافی به a نزدیک شود. در این صورت مینویسیم:

lim┬(x→a-)⁡〖f(x)=L〗

شرط وجود حد: تابع f در x=a حد دارد، اگر و تنها اگر حد چپ وراست تابع در x=a موجود و با هم برابر باشند. اگر حد چپ و راست هر دو باشند اما برابر یکدیگر نشوند تابع در این نقطه حد نخواهد داشت.

 قضایا حد

🔵برای مطالعه ادامه درسنامه لطفا جزوه را از فایل ضمیمه دانلود کنید 🔵

🔵عضویت در کانال تلگرام کانون برترها🔵