حد نامتناهی و حد در بی‌نهایت-حسابان-درسنامه- سروش اسماعیلی

دانش آموزان عزیز سلام 

در این مطلب مرور کامل بر مبحث حد از حسابان دوازدهم به همراه حل تست کنکور داریم. 

امیدوارم که این مطالب برای شما مفید باشد.

🟣ویژگی های مطلب🟣 

1- درسنامه کامل به همراه مثال و نکات‌ تابع 

2- 5 تست شناسنامه دار از این مبحث

3-پاسخ کلیدی تست ها در انتهای مطلب

4- ویدئو  و تدریس پاسخ تشریحی تست ها

مولف: سروش اسماعیلی  رتبه 395 کنکور ریاضی 1402 دانشجوی مهندسی مکانیک دانشگاه تهران

در ابتدا سوالات مهمی که از این بخش در امتحانات نهایی 1403  آمده است را مرور میکنیم تا اهمیت مبحث درک شود.

حال به سراغ درسنامه حد بینهایت میرویم

تعریف lim┬(x→a)⁡〖f(x)=+∞〗: یعنی  می‌توانیم f(x) را هر قدر بخواهیم از هر عدد مثبت بزرگتر کنیم به شرطی که x را به اندازه کافی به a میل بدهیم.(فرض کنیم f در یک همسایگی a تعریف شده باشد.)

تعریف lim┬(x→a)⁡〖f(x)=-∞〗: یعنی  می‌توانیم f(x) را هر قدر بخواهیم از هر عدد منفی کوچکتر کنیم به شرطی که x را به اندازه کافی به a میل بدهیم.(فرض کنیم f در یک همسایگی a تعریف شده باشد.)

برای مثال به نمودار تابع f(x)=1/(|x|)    توجه کنید. از هر سمتی به صفر میل کنیم مقدار تابع بدون هیچ محدودیتی افزایش می‌یابد. اما برای تابع g(X)=1/x وابسته به اینکه از سمت چپ یا راست به سمت صفر میل میکنیم اندازه تابع به ترتیب بدون محدودیت کاهش یا افزایش می‌یابد.پس میتوانیم برای حدود نامتناهی حد چپ و راست نیز تعریف کنیم.

تعریف lim┬(x→+∞)⁡〖f(x)=l〗: یعنی  می‌توانیم f(x) را هر قدر بخواهیم به L نزدیکتر کنیم به شرطی که x را به اندازه کافی بزرگ کنیم.(فرض کنیم f روی بازه (a,+∞)تعریف شده باشد.)

تعریف lim┬(x→-∞)⁡〖f(x)=l〗: یعنی  می‌توانیم f(x) را هر قدر بخواهیم به L نزدیکتر کنیم به شرطی که x را به اندازه کافی کوچک کنیم.(فرض کنیم f روی بازه (-∞,a)تعریف شده باشد.)

برای مثال به نمودار تابع f(x)=1/(|x|)    توجه کنید. از هر سمتی به بینهایت میل کنیم مقدار تابع 0 از سمت مثبت نزدیک و نزدیکتر میشود. اما برای تابع g(X)=1/x وابسته به اینکه به سمت مثبت بینهایت یا منفی بینهایت میل میکنیم اندازه تابع به ترتیب به صفر مثبت یا صفر منفی نزدیک میشود.

🔵برای مطالعه ادامه درسنامه میتوانید جزوه را از فایل ضمیمه دانلود کنید🔵 

در آخر 5 تست از کنکور سال‌های اخیر را به همراه پاسخ کلیدی 

 برای‌تان قرار داده‌ایم 

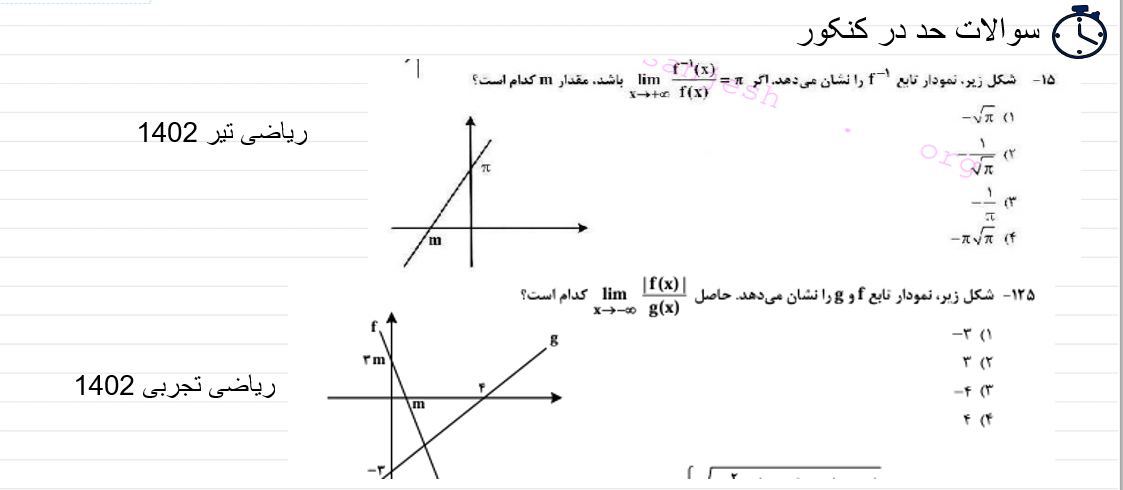
✨برای مشاهده پاسخ تشریحی و  تحلیل تست ها  میتوانید اینجا کلیک کنید.✨

🔵عضویت در کانال تلگرام کانون برترها🔵