سلام به همه نهمی های عزیز 🖐🖐
در این مطلب به فصل ششم کتاب ریاضی نهم میپردازیم.

🔴ویژگیهای مطلب🔴
درسنامه کامل و نکات
مثال های فراوان
پاسخ کلیدی و تشریحی در فایل ضمیمه
معادله خط : رابطه ای است که بین نقاط تشکیل دهنده یک خط وجود دارد.
نکته : فرم کلی معادله خط به صورت (𝑦 = 𝑎𝑥 + 𝑏) می باشد.
مثال : آیا رابطه بین یک ضلع مربع و مساحت مربع رابطه ی خطی است؟ چرا؟
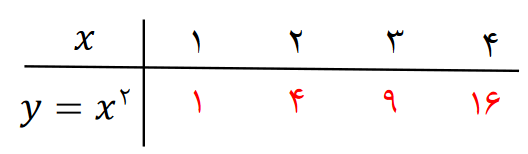
پاسخ تشریحی: خیر. چون افزایش یک ضلع مربع با افزایش مساحت مربع مقدار ثابتی نیست.
انواع معادله خط :
- 1.مبدا گذر (𝒚 = 𝒂𝒙 ∶ کلی فرم)
- 2.غیر مبدا گذر (𝒚 = 𝒂𝒙 + 𝒃 ∶ کلی فرم)
- 3.خطوط موازی با محور (𝒚 = b , 𝒙 = a ∶ کلی فرم)
رسم یک خط : برای رسم یک خط در دستگاه مختصات نیاز به مختصات دو نقطه است.
مثال : معادله خط y=4x را در دستگاه مختصات رسم کنید.
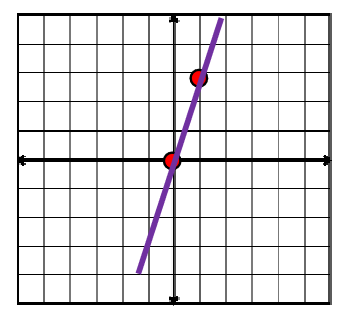
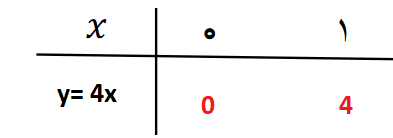
نکته : شرط این که نقطه روی یک خط قرار گیرد این است که مختصات آن نقطه در معادله خط صدق کند.که برای این کار دو روش وجود دارد :
1) روش تحلیلی(جایگزینی مختصات نقطه در معادله خط)
2) روش ترسیمی
شیب خط : زاویه ای بین سمت راست محور طول ها با خط داده شده را می گویند.
عرض از مبدا : نقطه ای که خط داده شده محور عرض ها را در آن نقطه قطع می کند را عرض از مبدا می گویند.
نکته : در فرم کلی معادله خط (𝒚 = 𝒂𝒙 + 𝒃) ضریب 𝒙 یعنی عدد 𝒂 شیب خطو عدد 𝒃 عرض از مبدا نام دارد.
نکته : برای به دست آوردن شیب خط و عرض مبدا باید معادله خط به فرم کلی (𝒚 = 𝒂𝒙 + 𝒃) مرتب شود.
مثال : شیب خط و عرض از مبدا معادله خطی زیر را به دست آورید؟
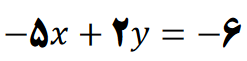
پاسخ تشریحی:
.
..
...
....
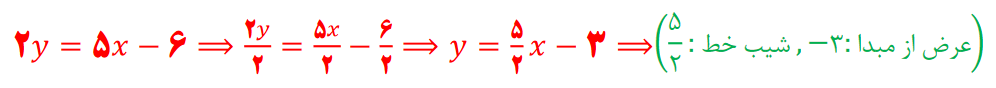
طول از مبدا : نقطه ای که خط داده شده محور طولها را در آن نقطه قطع می کند راطول از مبدا می گویند.
نکته : دو خط در صورتی موازی هستند که شیب دو خط برابر باشند.
نکته : دو خط در صورتی بر هم عمود هستند که شیب دو خط قرینه و معکوس یکدیگر باشند یا حاصل ضرب دو شیب خط برابر باعدد 1- شود.
دستگاه معادلات خطی : برای حل دستگاه معادلات خطی از روش های زیر می توان استفاده کرد :
الف) روش حذفی : در این روش یکی از متغیرهارا حذف کرده سپس با جایگزینی متغیر دوم به دست می آید.
ب) روش جایگزینی(تبدیلی): در این روش یکی از معادلات را بر حسب یک متغیرمرتب کرده و مقدار آن را در معادله دوم قرار می دهیم.
مثال : سن برادر علی 3 برابر سن او است و اختلاف سن آن ها 11 سال است. سن هر یک را به دست آورید.
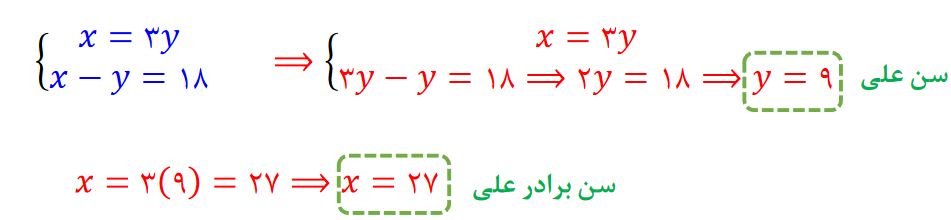
و حالا وقت تسته!!!




برای ارتباط با پشتیبان ویژه و اطلاع از شرایط مشاوره با رتبه هاي برتركانوني
به لينك زير مراجعه كنيد.


