ریاضی هشتم فصل سوم - درسنامه کامل+تست - علی اشرفپور

سلام به همه هشتمی های عزیز 🖐🖐

در این مطلب به فصل سوم کتاب ریاضی هشتم می‌پردازیم.

🔴ویژگی‌های مطلب🔴

درسنامه کامل و نکات

مثال های فراوان 

پاسخ کلیدی و تشریحی در فایل ضمیمه

چند ضلعی :

به هر خط شکسته بسته ای به شرطی که اضلاع آن همدیگر را قطع نکند چند ضلعی می گویند.

چند ضلعی منتظم :

چند ضلعی که تمام اضلاع و تمام زاویه های آن با هم مساوی باشند.

چند ضلعی محدب :

چند ضلعی که تمام زاویه های آن از 180 درجه کمتر باشد.

چند ضلعی مقعر :

چند ضلعی که حداقل یکی از زاویه های آن از 180 درجه بیشترباشد.

نکته : اگر در یک چند ضلعی دو نقطه دلخواه انتخاب کنیم و آن دو نقطه را بایک خط راست به هم وصل کنیم اگر قسمتی از خط بیرون از چند ضلعی قرار گرفت آن چندضلعی مقعر است،اگر تمام خط داخل چند ضلعی قرار گرفت چند ضلعی محدب است.

مرکز تقارن :

اگر دوران 180 درجه شکلی حول یک نقطه از شکل روی خود شکل قرار گیرد آن شکل مرکز تقارن دارد.

نکته : برای این که بدانیم شکلی مرکز تقارن دارد یا نه . نقطه ای در وسط شکل به عنوان مرکز تقارن در نظر گرفته سپس از شکل نقاطی به دلخواه انتخاب کرده به مرکزتقارن وصل و به همان اندازه ادامه می دهیم اگر نقطه حاصل روی شکل قرار گرفت آن شکل مرکز تقارن دارد.در غیر این صورت آن شکل مرکز تقارن ندارد.

نکته : در چند ضلعی منظم اگر تعداد اضلاع زوج باشد مرکز تقارن دارد و اگر فرد باشد مرکز تقارن ندارد.

محور تقارن (خط تقارن) :

خطی است که اگر کاغذ را تا کنیم همه نقاط شکل روی هم قرار می گیرند.

نکته : خط تقارن خطی است که چند ضلعی رابه دو قسمت مساوی تقسیم کند.

نکته : چند ضلعی های منتظم به تعداد اضلاع محور تقارن دارند.

مثال : هر یک از چند ضلعی های زیر چند محور تقارن دارد؟ 

دو خط موازی :

دو خطی که هر چه آن ها را امتداد دهیم همدیگر را قطع نکنند و فاصله بین دو خط تغییر نکند دو خط موازی می گویند.

دو خط متقاطع :

دو خطی که موازی نباشند یعنی دو خطی که همدیگر را در نقطه ای قطع کنند دو خط متقاطع می گویند.

دو خط عمود بر هم :

دو خط متقاطعی که زاویه بین دو خط 90 درجه باشد.

مثال : در هر شکل مقدار  𝒙 را به دست آورید؟

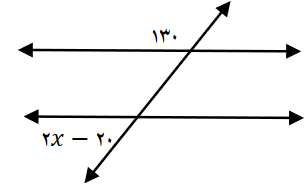
پاسخ تشریحی:

2X+(-20)+130=180 =>2X=70 => X=75

انواع چهار ضلعی ها :   

1) متوازی الاضلاع      2) مستطیل          3) مربع                 4) لوزی              5) ذوزنقه

متوازی الاضلاع :

چهار ضلعی است که اضلاع روبه رو موازی و مساویند.

خواص متوازی الاضلاع :           1) اضالاع روبه رو موازی و مساویند              2) زاویه های روبه رو مساویند   

                       3) قطرهای متوازی الاضلاع همدیگر را نصف می کنند                   4) زاویه های مجاور (کنارهم) مکمل اند

مستطیل :

متوازی الاضلاعی است که زاویه قائمه داشته باشد.

خواص مستطیل :       1) تمام خواص متوازی الاضلاع را دارد               2) دو قطر مستطیل برابرند

مربع :

متوازی الاضلاعی است که چهار ضلع آن برابر و زاویه قائمه داشته باشد.

خواص مربع :      1) تمام خواص متوازی الاضلاع را دارد  2) دو قطر مربع برابرند  3)قطرهای مربع عمود منصف یکدیگرند

لوزی :

متوازی الاضلاعی است که چهار ضلع آن برابر است.

خواص لوزی :          1) تمام خواص متوازی الاضلاع را دارد            2) قطرهای لوزی عمود منصف یکدیگرند

ذوزنقه : 

چهار ضلعی است که فقط دو ضلع موازی دارد.

انواع ذوزنقه :          1) ذوزنقه متساوی الساقین                   2) ذوزنقه قائم الزاویه

خواص ذوزنقه متساوی الساقین :             1) دو ساق آن برابرند              2) دو زاویه مجاور قاعده برابرند

                                                                          3) دو زاویه مجاور ساق مکمل اند

خواص ذوزنقه قائم الزاویه :                     1) دارای زاویه قائمه است

نکته : مجموع زاویه های داخلی مثلث 180 درجه است.

نکته : مجموع زاویه های داخلی چند ضلعی از رابطه ی (𝑛 − 2) 180 حاصل می شود.

نکته : اندازه ی یک زاویه ی چند ضلعی منتظم از رابطه ی    حاصل می شود.

زاویه خارجی :

اگر یکی از اضلاع چند ضلعی محدب را در همان راستا امتداد دهیم در بیرون از چند ضلعی زاویه ای تشکیل می شود که به آن زاویه خارجی چند ضلعی می گویند.

نکته : در هر مثلث اندازه ی زاویه خارجی برابر است با مجموع دو زاویه داخلی غیر مجاور آن.

نکته : مجموع زاویه های خارجی هر چند ضلعی 360 درجه است.

نکته : اندازه ی یک زاویه خارجی چند ضلعی منتظم از رابطه ی    حاصل می شود.

و حالا وقت تسته :)

برای ارتباط با پشتیبان ویژه و اطلاع از شرایط مشاوره با رتبه هاي برتركانوني 

به لينك زير مراجعه كنيد.

ارتباط با پشتیبان ویژه