
سلام به همه بچههای علاقمند به کامپیوتر و برنامهنویسی و هوش مصنوعی. همانطور که میدونین روز به روز دنیای هوش مصنوعی داره وسیعتر میشه و به حوزه مختلف از علوم راه یافته است. ما تصمیم داریم هر هفته با یک مقاله در این حوزه، شمارو با رویداد های دنیای هوش مصنوعی آشنا کنیم و مهمتر اینکه ریاضیات این حوزه رو با ساده سازی به شما دانش آموزان عزیز کانونی توضیح بدیم. در نهایت بتونیم قدم به قدم به کد نویسی در محیط پایتون برای مسئله های جذاب هوش مصنوعی برسیم. پیشنهاد میکنم هر هفته مارو با یک مقاله در این حوزه دنبال کنید.
هفته پیش در مورد خاصیت چکههای آب با هم صحبت کردیم. اینکه حرکت قطره آب روی خاک چجوریه و این حرکت چه ارتباطی با میزان خاک موجود در اون بخش و سرعت جریان آب داره. این هفته میخواییم بحث رو یه کمی ریاضیاتی کنیم و همون مطالب رو با محاسبات ریاضی بیان کنیم.
یک چکه آب هوشمند (IWD) تو مسافتهای محدود و جداگانه حرکت میکنه. یعنی شتاب IWD از نقطه i تا نقطه j به واسطه دلتای شتاب (Δvelocity) افزایش پیدا میکنه که این دلتا به طور غیر خطی متناسب است با معکوس مقدار خاک بین دو نقطه مذکور. یعنی هر چی اون یکی بیشتر باشه این یکی کمتر و بالعکس. فرمولشو ببنید قطعاً متوجه میشید قضیه از چه قراره:
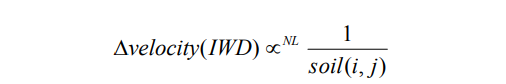
حواستون باشه که اینجا منظور ما از ∝NL همون تناسب غیر خطی است. یه فرمول محتمل دیگه این پایین میاریم که باهاش شتابِ IWD (velIWD(t)) رو به وسیله میزان خاک موجود بین دو نقطه i , j محاسبه میکنیم:
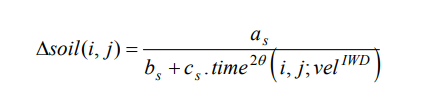
اینجا منظور از av , vb , vc و α پارامترهای مثبتیه که یوزر ازشون استفاده میکنه.
بعلاوه خاکِ IWD (soil(IWD)) با حذف شدن مقداری از خاک موجود در مسیر i , j افزایش پیدا میکنه. مقدار خاک اضافه شده به IWD (Δsoil(IWD)= Δsoil(i,j)) یک تناسب معکوسی داره با میزان زمانی که طول میکشه IWD از مسیر مورد نظرمون بگذره. باز هم یعنی اگه خاک بیشتر باشه زمان کمی طول میکشه و بالعکس:
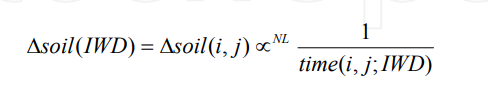
بچه به تناسبهای جالب بین چکه اب و خاک، خاک و مقدار زمان، چکه آب و مقدار زمان حتما توجه داشته باشید تا نظم زیبای بین فرایندهای گذشتن یه قطره آب رو مشاهده کنید.
یه راه برای بهبود فرمول بالا میتونه فرمول پایین باشه که در اون time(i,j;velIWD) زمانی رو نشون میده که IWD نیاز داره (velIWD) تا از نقطه i به نقطه j برسه. خاکی که به IWD اضافه میشه اینجوری محاسبه میشه:
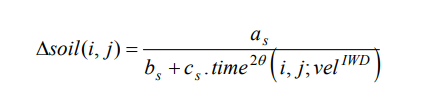
دیرند (duration) زمان برای IWD با قوانین ساده فیزیک درباه حرکت خطی سنجیده میشه. بنابراین، زمانی که IWD لازم داره تا از دو نقطه فرضیمون رد بشه متناسب است با شتاب IWD ،یعنی velocity (IWD)، و همچنین تناسب معکوس داره با فاصله بین دو نقطه. به زبان ریاضی:
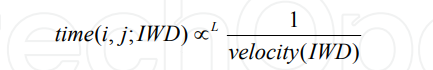
حواستون باشه که ∝L به معنی تناسب خطی است. یه فرمول دیگهای که پایین آوردیم مقدار زمان مورد نیاز IWD رو برای حرکت از نقطه i به نقطه j با شتاب velIWD نشون میده:
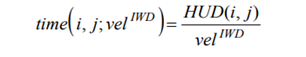
اینجا HUD(.,.) یعنی میزان هزینهی لازم برای انتقال از جایی به جای دیگر که برای تعیین نامطلوبیت (undesirability) حرکت یک IWD از نقطهای به نقطهی دیگر استفاده میشه. لب کلام این که اگه یه راه HUD بالایی داشته باشه IWD کمتر میل داره از اون عبور کنه.
وقتی IWD از یه مسیر میگذره خاک موجود در اون مسیر رو میشوره و خاک جدید جایگزین اونای قبلی میشه. خاک تازه که با soil(i , j) نشون میدیم متناسب است با میزان خاکی که از بین رفته. خلاصه به زبون ریاضی یعنی Δsoil(i,j)= Δsoil(IWD):
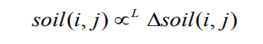
از فرمول بالا برای الگریتم IWD (چکههای آب هوشمند)استفاده میکنیم به طوری که soil ( j,i ) به واسطه میزان خاکی که IWD تو مسیرش از بین برده آپدیت میشه:
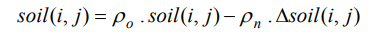
ρo و ρnغالباً اعداد مثبتی هستند بین صفر و یک.
همینجا مطلبمون رو به پایان میبریم. امیدواریم تا هفته بعد و مطلب بعد مقاله این هفته و هفته پیش رو خوب مرور بکنید تا بتونیم هر چه دقیقتر و مطلوبتر جلو بریم.

منابع
Optimization with the Nature-Inspired Intelligent Water Drops Algorithm, Hamed Shah-Hosseini
دوستان عزیزم؛ برای ارتباط با برترها و رزرو پشتیبان ویژه پیج کانون برترها را دنبال کنید.
همچنین میتوانید با شماره 0218451 داخلی 3123 تماس بگیرید.



