
سلام به همه بچههای علاقمند به کامپیوتر و برنامهنویسی و هوش مصنوعی. همانطور که میدونین روز به روز دنیای هوش مصنوعی داره وسیعتر میشه و به حوزه مختلف از علوم راه یافته است. ما تصمیم داریم هر هفته با یک مقاله در این حوزه، شمارو با رویداد های دنیای هوش مصنوعی آشنا کنیم و مهمتر اینکه ریاضیات این حوزه رو با ساده سازی به شما دانش آموزان عزیز کانونی توضیح بدیم. در نهایت بتونیم قدم به قدم به کد نویسی در محیط پایتون برای مسئله های جذاب هوش مصنوعی برسیم. پیشنهاد میکنم هر هفته مارو با یک مقاله در این حوزه دنبال کنید.
شبکه های عصبی غیر خطی
خب دوستان، در جلسه قبل در مورد تقسیم بندی شبکه های عصبی صحبت کردیم و گفتیم که این شبکه ها رو میشه به دو حالت خطی و غیر خطی تقسیم بندی کرد. در جلسه قبل، در مورد شبکه های خطی صحبت کردیم و در این مقاله هم میخوایم شبکه های غیر خطی رو مورد مطالعمون قرار بدیم. اما قبلش بهتره در چند سطر یه مروری از مباحث هفته قبل داشته باشیم.
گفتیم که یکی از کارهای مهمی که بسیاری از الگوریتم های شبکه های عصبی انجام میدن، دسته بندی داده های ورودی هستش. مسئولیت اصلی این کار بر عهده تابع فعال ساز شبکه ها هست که در مورد این توابع در مباحث هفته قبل صحبت داشتیم. اما موقع انتخاب تابع فعال ساز برای شبکه مون باید به ورودی هامون و خروجی که میخوایم از این ورودی ها بگیریم، توجه کنیم. در برخی از موارد، داده های ورودی رو میشه با یک تابع خطی از هم تفکیک کرد، مثلا فرض کنید گروهی از اعداد مثبت و منفی رو به عنوان ورودی داریم و میخوایم این اعداد مثبت و منفی رو از هم جدا کنیم. خب کاری که میتونیم انجام بدیم اینه که از تابع sign استفاده کنیم. چون تابع sign اعداد مثبت و منفی رو از هم جدا میکنه. خب بزارید یه مثال دیگه رو هم بررسی کنیم. داده های موجود در محور فضای مختصات شکل زیر رو در نظر بگیرید. داده های موجود بر اساس مقدار مختصاتی که دارن، به دو دسته آبی و قرمز تقسیم شدن.
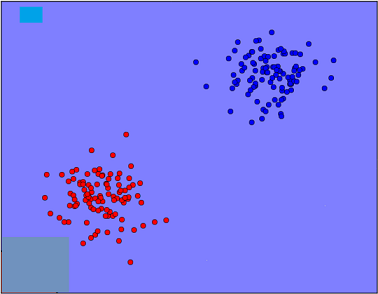
حالا فرض کنید میخایم یه شبکه ای داشته باشیم که داده های قرمز و آبی رو از هم تفکیک کنه، و یا مثلا داده های قرمز رو به عنوان خروجی به ما بده و داده های آبی رو برامون فیلتر کنه. از ظاهر شکل معلوم و مشخص هست که میشه داده ها رو به صورت خطی از هم جدا کرد. پس میشه گفت که داده هامون قابلیت دسته بندی به صورت خطی رو دارن و از شبکه عصبی خطی باید استفاده کنیم؛ یا به عبارت دقیق تر، باید از یک تابع فعال ساز خطی استفاده کنیم. برای مثال میتونیم از تابع زیر استفاده کنیم:
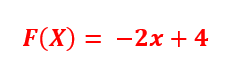
که در نتیجه پس قرار دادن تابع فعال ساز در شبکه و ایجاد شبکه عصبی، خواهیم داشت:
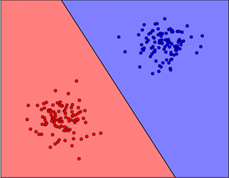
خب شاید الان در ذهنتون این سوال پیش بیاد که این نوع دسته بندی خیلی ساده هست و اصلا چه نیازی به شبکه های پیچیده عصبی هستش! در جواب باید بگیم که داده ها معمولا این طوری ساده توزیع نمیشن. و دسته بندی اون ها روند خیلی پیچیده تری رو میخاد که در اغلب موارد به باید به صورت غیر خطی جدا شن. در شکل زیر، برخی از این داده ها رو میتونید ببنید که نمیشه به صورت خطی از هم تفکیک بشن :
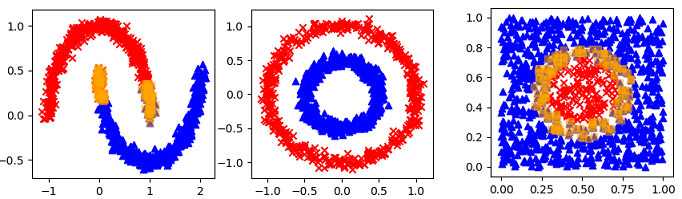
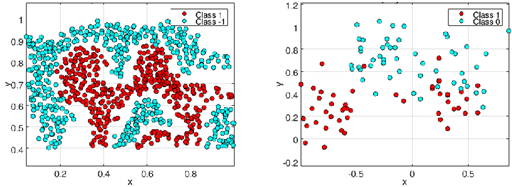
خب الان به نظرتون چطوری میشه داده های غیر خطی و پیچیده رو تفکیک و دسته بندی کرد؟
در برخی موارد، داده ها به طریقی توزیع شده ان که میشه از با استفاده از تنها یک تابع غیر خطی این تفکیک صورت بگیره ( برای مثال با استفاده از توابع نمایی در توابع فعال ساز) . اما به طور کلی، باید از ترکیب توابع مختلف برای این کار بهره برد. در این جلسه، میخوایم مثالی رو بررسی کنیم که در اون از طریق ترکیب توابع خطی، دسته بندی غیر خطی صورت گرفته است.
دسته بندی غیر خطی از طریق ترکیب توابع خطی
برای درک این مسئله، به یک مثال ساده توجه کنید. داده های زیر رو در نظر بگیرید و فرض کنید که میخوایم داده های سبز رو از داده های نارنجی تفکیک کنیم. مسلما نمیتونیم روش خطی استفادع کنیم. تابع غیر خطی مشخصی هم نداریم که بتونه مثل منحی سیاهی که کشیده شده، داده ها رو از هم جدا کنه. پس باید از ترکیب توابع استفاده کنیم.
نتیجه ترکیب توابعمون باید در نهایت، شکلی شبیه به شکل منحی سیاه رو به ما بده. در قدم اول، دو مدل خطی پیدا میکنیم که با ترکیب اونا مدلی مانند مدل زیر به دست بیاد:

در مرحله بعدی، ابتدا به هر کدوم از مدل های خطی یه اسمی مانند x1 و x2 رو اختصاص میدیم. بعد برای هر کدوم از توابع ورودیمون یه ضرایبی مانند w1 و w2 رو در نظر میگیریم. این ضرایب، برای تنظیم ورودی هامون هستند که بتونیم با تغییر ضرایب، توابع ورودی رو جابهجا کنیم. یک ضریب کلی بایاس هم برای کل توابع ورودیمون در نظر میگیریم که با تغییر این ضریب، کل توابع و اندازهها تغییر میکنن. خواهیم داشت:
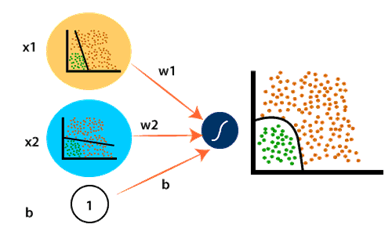
میبینم که توابع x1 و x2 با وزن w1 و w2 و بایاس b ، از یک تابع نمایی عبور کرده و تونسته که داده های سبز رنگ رو از داده های نارنجی رنگ دسته بندی کنه.
خب حالا سوال پیش میاد که این ضرایب و بایاسی که هست به چه دردی میخوره؟ فرض کنید به جای x1 ، 1.5 ، به جای x2 ، 1 و به جای ضریب بایاس هم عدد 0.5 رو اختصاص دادیم و نتیجه به صورت شکل زیر بدست اومده.
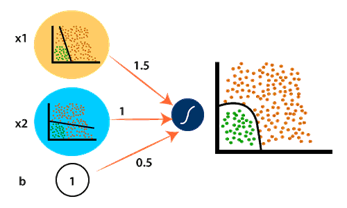
اگه مقدار ضریب x1 رو بیشتر کنیم، داده های بیشتری رو در راستای طولی درون منحنی جا میدیم و اگه ضریب x2 رو بیشتر کنیم، منحی در راستای عرضی داده های بیشتری رو پوشش میده . برای مثال، اگه به جای ضریب w2 که در ساختار بالا یک هست، ضریب 3 رو قرار بدیم، منحنی ما به شکل زیر تبدیل خواهد شد:
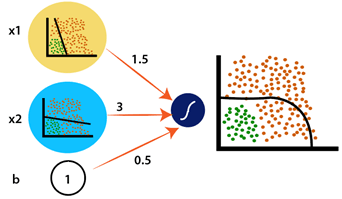
پس ما تونستیم با ترکیب دو تابع خطی و چند ضریب، یک دسته بندی غیر خطی رو انجام بدیم و با ساختار دسته بندی غیر خطی بیشتر آشنا بشیم . در جلسات آینده، به این بحث خواهیم رسید که این توابع خطی و ضرایب رو چطور به صورت عملی در بستر شبکه های عصبی پیاده کنیم . پس با ما همراه باشید...
منابع
https://www.javatpoint.com/pytorch-non-linear-boundary-in-deep-neural-network
http://www.briandolhansky.com/blog/2013/7/11/artificial-neural-networks-linear-classification-part-2
کلیدواژهها

دوستان عزیزم؛ برای ارتباط با برترها و رزرو پشتیبان ویژه پیج کانون برترها را دنبال کنید.
همچنین میتوانید با شماره 0218451 داخلی 3123 تماس بگیرید.



