مساحت و کاربرد _ هندسه دهم _ خلاصه و نکات درسی _ فاضل مهرآئین

سلام دوستان ! ✋

در این مطلب قصد داریم بخش سهمی از مساحت و کاربردها را در قالب درسنامه و تست بررسی کنیم.

در این مطلب پنج تست از مبحث فوق قرار دادیم .

 اگر سوالی از این مطلب دارید در قسمت کامنت ها بپرسید .

برای دریافت پاسخ تشریحی ، مطلب را از قسمت فایل های ضمیمه دانلود کنید.

فاضل مهرآئین - دانشجوی مهندسی مکانیک صنعتی شریف - رتبه 333 منطقه یک

مساحت مثلث برابر است با نصف اندازه یک ضلع مثلث در طول ارتفاع وارد بر این ضلع. در نتیجه می توان گفت که در هر مثلث، کوتاه ترین ارتفاع، بر بزرگ ترین ضلع وارد می شود و بالعکس.

ارتفاع مثلث متساوی الاضلاع به طول ضلع a برابر 2 /3√a  است.

مساحت مثلث متساوی الاضلاع به طول ضلع   برابر 4 /3√2^a است.

دستور مثلثاتی مساحت مثلث: مساحت مثلث برابر است با نصف حاصل ضرب طول های دو ضلع در سینوس زاویه بین آنها:

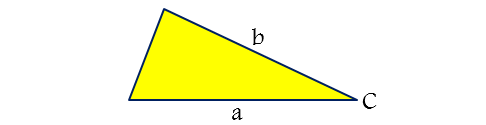
S=(0.5)(a)(b)sin(C)

مساحت متوازی الاضلاع برابر است با حاصل ضرب طول یک ضلع در طول ارتفاع وارد بر آن ضلع:

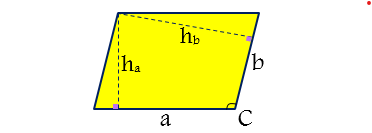
S=(a)(ha)=(b)(hb)

برای محاسبه مساحت متوازی الاضلاع یک دستور مثلثاتی نیز وجود دارد که به طریق زیر است(شکل بالا):

S=(a)(b)sin(C)

دستور مثلثاتی برای مساحت چهارضلعی ها: مساحت چهارضلعی برابر است با نصف حاصل ضرب طول قطرها در سینوس زاویه بین دو قطر:

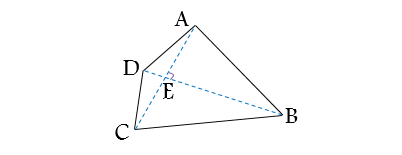
S=(0.5)(AC)(BD)sin(E)

مساحت ذوزنقه برابر است با نصف مجموع طول های قاعده هایش ضرب در طول ارتفاعش:

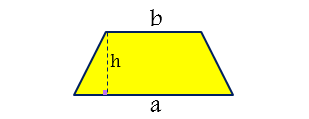
S=(0.5)(a+b)(h)

توجه: در هر مثلث، هر میانه، مساحت مثلث را نصف می کند.

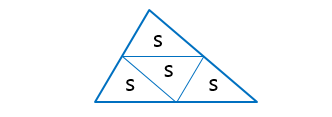
نکته: اگر وسط اضلاع مثلثی را با خطوطی به هم وصل کنیم، چهار مثلث همنهشت (و هم مساحت) ایجاد می شود:

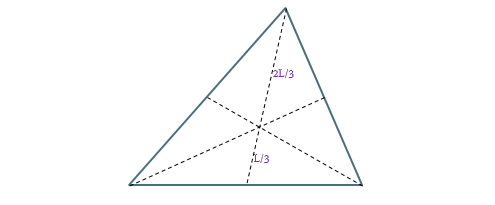
قضیه: سه میانه مثلث در نقطه ای درون آن همرس هستند و این نقطه میانه ها را به نسبت 1 به 2 تقسیم می کند. به این ترتیب، فاصله نقطه همرسی میانه ها تا وسط هر ضلع برابر 1/3 طول میانه نظیر این ضلع است و فاصله اش تا هر راس برابر با 2/3 طول میانه نظیر این راس است:

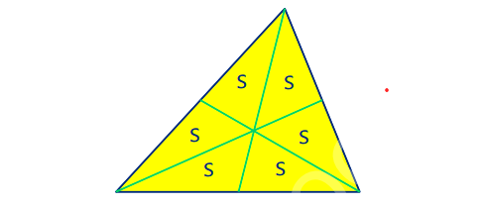
میانه های یک مثلث آن را به 6 مثلث با مساحت های مساوی تقسیم می کنند:

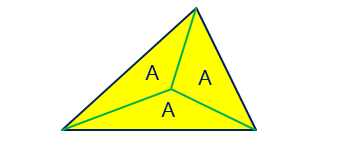
در هر مثلث اگر از نقطه همرسی میانه ها به رئوس آن وصل کنیم، 3 مثلث با مساحت های مساوی پدید می آیند:

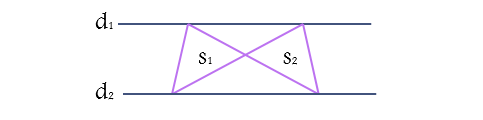
قضیه شبه پروانه

در شکل زیر اگر دو خط d1 و d2 موازی باشند، داریم: s1=s2

تست ها 

در هر مثلث متساوی الساقین، مجمموع فاصله های هر نقطه دلخواه روی قاعده از ساقین برابر با کدام است؟ (متوسط)

1) طول ارتفاع وارد بر ساق

2) طول ارتفاع وارد بر قاعده

3) طول ساق

4) طول قاعده 

در مربعی به طول ضلع 12، روی اضلاع مقابل مثلث های متساوی الاضلاع رسم شده اند و به تبع آن یک لوزی درون مربع پدید آمده. طول قطر بزرگ لوزی حدودا کدام است؟ (متوسط)

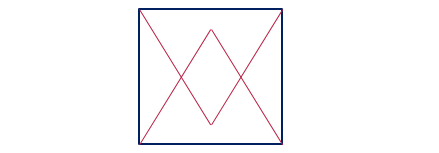
1) 8.8

2) 3.6

3) 1.8

4) 8.4

در شکل زیر ،دو میانه رسم شده بر هم عمودند. طول یکی از آنها 9 و دیگری 6 است. مساحت بزرگ ترین مثلث کدام است؟ (متوسط)

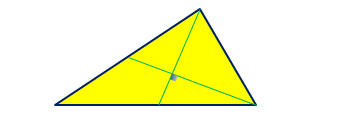
1) 18                     2) 72                           3) 36                       4) 54

در مثلث نشان داده شده D و E وسط اضلاع هستند. همچنین F وسط BD و G وسط BE است. مساحت بزرگ ترین ترین مثلث چند برابر بزرگ تر از کوچک ترین مثلث است؟ (متوسط)

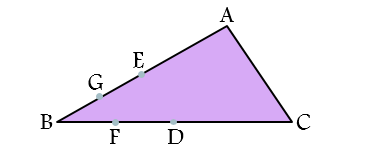
1) 8                2) 16                     3) 32                 4) نمی توان مشخص کرد.

اندازه اضلاع قائم مثلثی 9 و 12 است. فاصله نقطه برخورد میانه با نقطه برخورد ارتفاع وارد بر وتر مثلث کدام است؟ (متوسط)

1) 4.41               2) 7.2                  3) 7.5               4) نمی توان مشخص کرد.

برای ارتباط بیشتر با برترها و رزرو پشتیبان ویژه، رتبه برترهای کانون قلمچی را دنبال کنید، 

همچنین می توانید با شماره ۰۲۱۸۴۵۱ داخلی ۳۱۲۳ تماس بگیرید.