دانش آموزان عزیز سلام
در این سری مطالب میخواهیم در چندبخش، مبحث مثلثات در سه سال دبیرستان را به طور کامل پوشش دهیم .
امیدوارم که این مطالب برای شما مفید باشد.
🟣ویژگی های مطلب🟣
1- درسنامه کامل به همراه مثال و نکات اتحادهای مثلثاتی
2- 5 تست شناسنامه دار از این مبحث
3-پاسخ کلیدی تست ها در انتهای مطلب
4- ویدئو و تدریس پاسخ تشریحی تست ها
 | مولف: سروش اسماعیلی رتبه 395 کنکور ریاضی 1402 دانشجوی مهندسی مکانیک دانشگاه تهران |
در ابتدا سوالات مهمی که از این بخش در امتحانات نهایی 1402 و 1403 آمده است را مرور میکنیم تا اهمیت مبحث درک شود.
سوالات امتحان نهایی مثلثات خرداد 1403
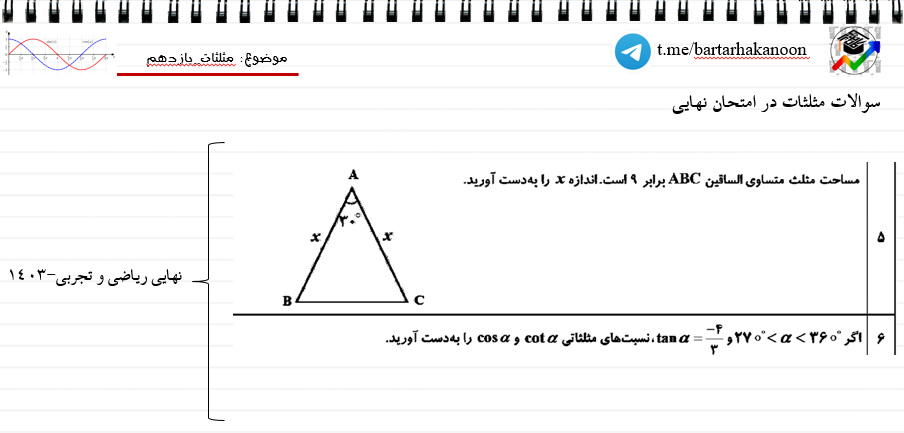
حال به سراغ درسنامه اتحاد های مثلثاتی میرویم:
روابط زیر بین نسبت های مثلثاتی برقرارند:
1. Sin2a+cos2a =1 2. tan a = sina/cosa 3. cot a = cosa/sina
4. tan a . cot a =1 5. cos2a = 1/"1+tan2a" 6. sin2a = 1/"1+cot2a"
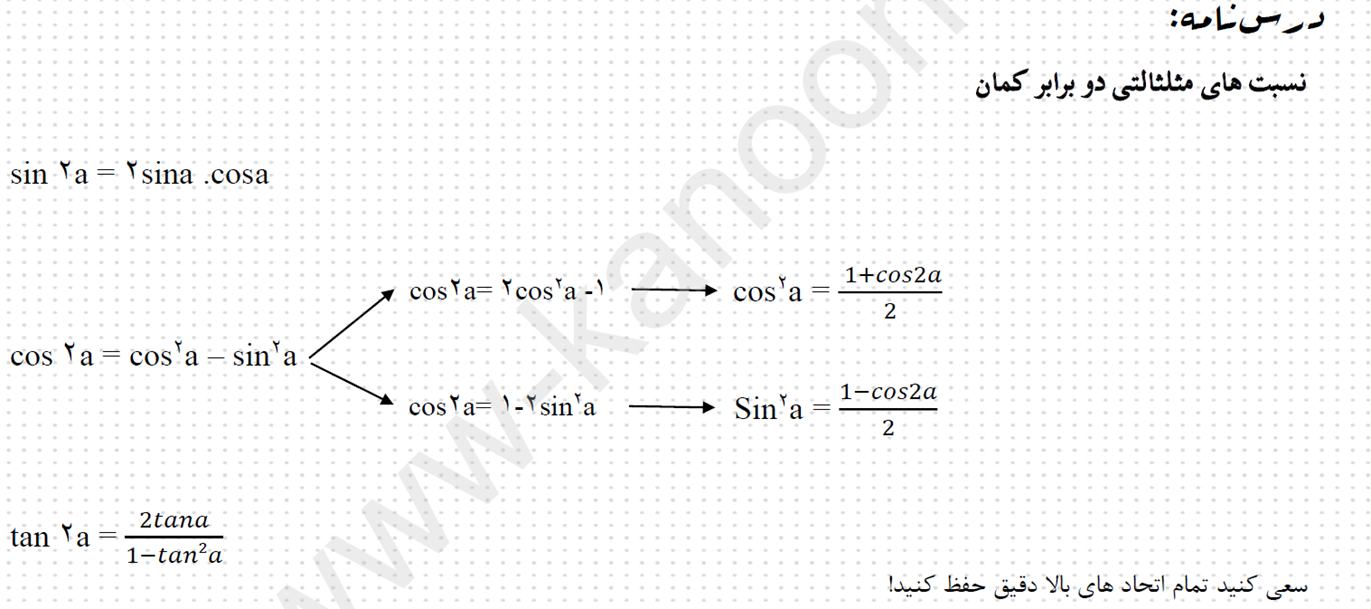
مجموع و تفاضل دو کمان
1.cos(a+b)= cosa .cosb - sina .sinb 2. cos(a-b)= cosa .cosb + sina .sinb
3.sin(a+b)= sina .cosb + cosa .sinb 4. sin(a-b)= sina .cosb - cosa .sinb
5. tan(a+b)=tan〖a+tanb 〗/(1-tan〖a .tanb 〗 ) 6. tan(a-b)=tan〖a-tanb 〗/(1+tan〖a .tanb 〗 )
دو اتحاد زیر پرکاربرد هستند:
1.Sinx + cosx = √2sin(x+π/4) 2.Sinx - cosx = √2sin(x-π/4)

تابع تانژانت
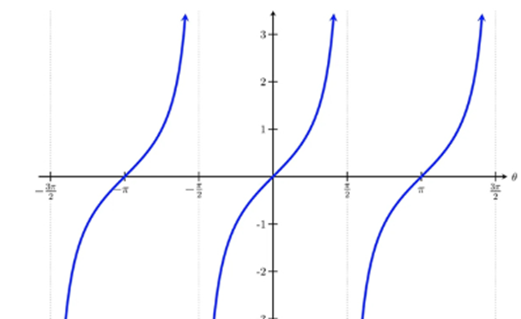
نمودار تانژانت در مجور های مختصات به شکل زیر است.
دامنه و برد تابع با توجه به نمودار به صورت مقابل است:
D=R-{kπ+π/2 | k∈z} R=R
تابع غیریکنوا است اما در هر بازه بین دو مجانب متوالی اکیدا صعودی است.
دوره تناوب تابع برابر میباشد و تابع حول مبدا مختصات متقارن است.
مثال) حاصل 1/sin10-√3/cos10 را بیابید.
ابتدا مخرج مشترک میگیریم و سپس در صورت از کسینوس جمع دو کمان کمک میگیریم:
= (cos10 -√3 sin10)/(sin10 cos10)= (2(1/2 cos10 -√3/2 sin10))/(sin10 cos10) = (2(cos60cos10 -sin60sin10))/(sin10 cos10) = (2(cos(60+10)))/(sin10 cos10)=2cos70/(1/2 sin20 ) = 4
مثال) اگر tan(p)=1/2 , q-p=π/4 باشد، مقدار sin(2q) را بیابید.
tan q =tan((q-p)+p)=(tan(q-p)+tanp)/(1-tan(q-p)tanp)= (1+0.5)/(1-0.5)=3 ⇒sin(2q)=2tanq/(1+tan2q) = (2(3))/(1+9)=0.6
🔵برای مطالعه کامل درسنامه میتوانید جزوه را از فایل ضمیمه دانلود کنید 🔵
🔵عضویت در کانال تلگرام کانون برترها🔵


