معادلات درجه دوم-درسنامه- سروش اسماعیلی

دانش آموزان عزیز سلام 

در این مطلب میخواهیم، مبحث معادلات درجه دو را به طور کامل پوشش دهیم .

امیدوارم که این مطلب برای شما مفید باشد.

🟣ویژگی های مطلب🟣 

1- درسنامه کامل به همراه مثال و نکات‌ معادله درجه دو

2- 5 تست شناسنامه دار از این مبحث

3-پاسخ کلیدی تست ها در انتهای مطلب

4- ویدئو  و تدریس پاسخ تشریحی تست ها

مولف: سروش اسماعیلی  رتبه 395 کنکور ریاضی 1402 دانشجوی مهندسی مکانیک دانشگاه تهران

درسنامه معادلات درجه دو و سهمی در ادامه آمده است:

معادله ax^2+bx+c=0 به شرطی که a≠0 باشد، یک معادله درجه دوم است. هر معادله از درجه n حداکثر تعداد n پاسخ یا همان ریشه دارد. پس یک معادله درجه 2 میتواند دو یا یک پاسخ داشته و یا هیچ ریشه‌ای نداشته باشد.

عبارت دلتا را با استفاده از ضرایب معادله بدین صورت تعریف میکنیم:

 Δ=b^2-4ac 

با دلتا میتوان تعداد و پاسخ‌ها را به دست آورد:

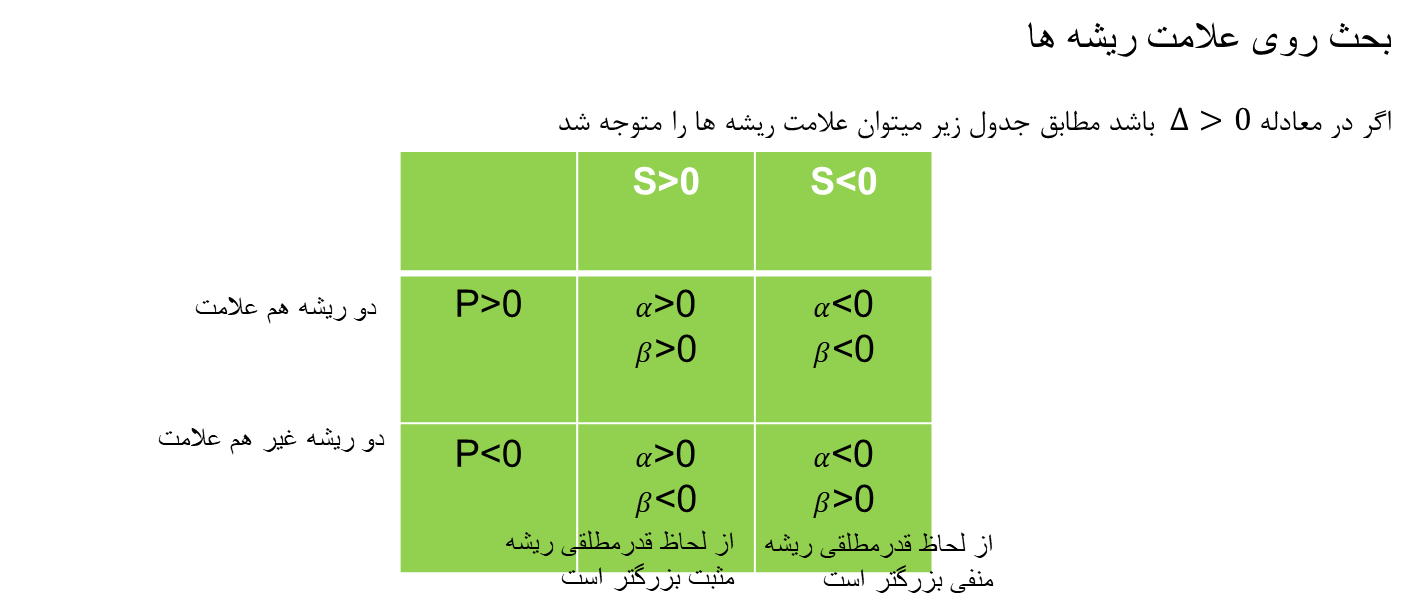
.1اگر  Δ >0باشد، معادله دو ریشه حقیقی متمایز دارد(با α و β نمایش میدهیم) که از رابطه زیر به دست می‌آیند:

α=(-b+√Δ)/2a                  β=(-b-√Δ)/2a

2.     اگر Δ=0  باشد، معادله یک ریشه مضاعف(مکرر مرتبه2) دارد یعنی یک ریشه که به نوعی دوبار پاسخ معادله است. این ریشه از رابطهα=(-b)/2a به دست می‌اید.

3.     اگر Δ<0  باشد، یعنی معادله هیچ ریشه حقیقی ندارد.(معادله ریشه از نوع اعداد مختلط(موهومی) دارد که در سطح کتاب دبیرستان نیست)

حل معادلات درجه 2 در شرایط خاص

گاهی حل از روش اصلی طولانی و سخت است و در شرایط زیر میتوان راه حل های سریعتری استفاده کرد:

●اگر مجموع ضرایب صفر شود یعنی a+b+c=0 آنگاه دو ریشه معادله برابرند با: ,  α=1 , β= c/a 

●اگر a+c=b باشند آنگاه دو ریشه معادله برابرند با: ,  α=-1 , β= (-c)/a 

●برخی اوقات با تجزیه و استفاده از اتحادهایی مانند جمله مشترک سریعتر به پاسخ میرسیم:

x^2-5x+6=0 => (x-3)(x-2)=0 => x1=2 , x2=3

روابط بین ضرایب و ریشه‌‌ها

در معادلات درجه 2 بدون داستن خود ریشه ها میتوان در مورد جمع یا ضرب و حتی علامت آنها بحث کرد

در یک معادله درجه 2 به صورت ax2+bx+c=0 که دو ریشه  α,βدارد میتوان گفت:

S= α+β = (-b)/a          ;   P= α∗β = c/a

به این ترتیب میتوان با داشتن ضرب و جمع ریشه ها معادله درجه 2 را به فرم زیر تشکیل داد:

x2-Sx+P=0      ó (x- α)(x- β)=0

در معادله‌ای که دو ریشه دارد(Δ >0) اگر b=0 باشد انگاه مجموع یعنی s نیز برابر صفر است پس دو ریشه قرینه یکدیگرند.

به همین شکل اگر a=c باشد انگاه p=1 میشود یعنی ضرب دو ریشه 1 شده پس معکوس یکدیگرند.

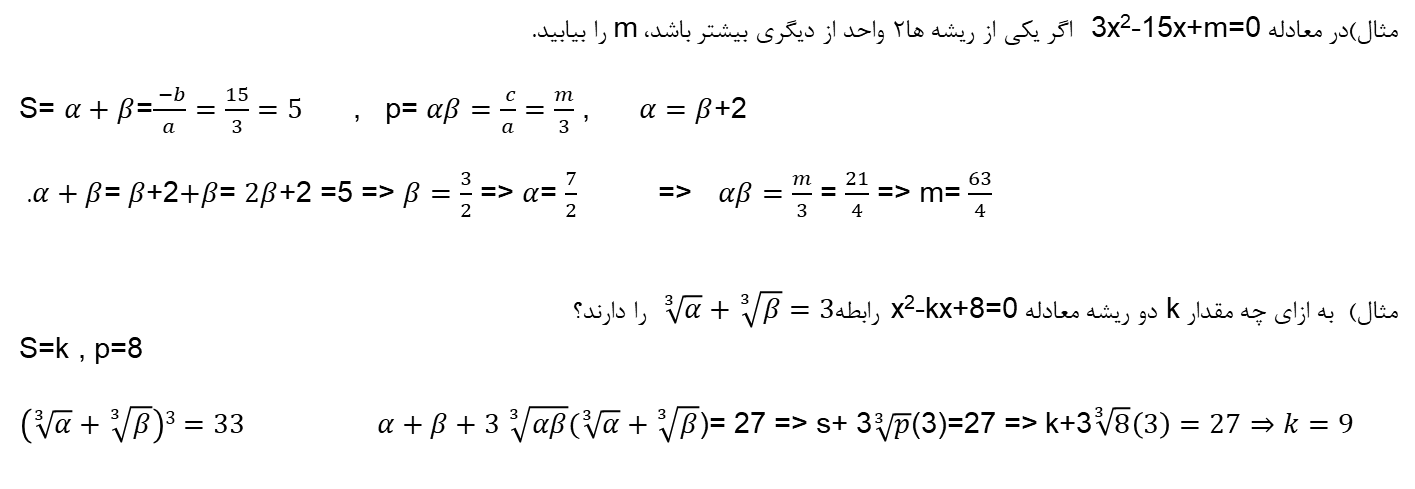
بحث روی علامت ضرایب از روی سهمی

•اگر سهمی رو به بالا باشد، a>0 و اگر رو به پایین باشد a<0 است.

•اگر طول راس سهمی سمت چپ محور y باشد یعنی (-b)/2a<0  و اگر سمت راست باشد یعنی (-b)/2a>0 ، چون علامت a در مرحله قبل تعیین شده در اینجا علامت b نیز مشخص میشود. اگر روی محور باشد هم (-b)/2a=0 پس b=0 است.

•c یعنی همان عرض از مبدا نشان دهنده محل برخورد سهمی با محور عرض ها است پس اگر محل برخورد بالا محور باشد یعنی c>0 و اگر پایین محور باشد یعنی c<0 است.

🔵برای مطالعه کامل درسنامه میتوانید جزوه را از فایل ضمیمه دانلود کنید 🔵

🔵عضویت در کانال تلگرام کانون برترها🔵