معادلات مثلثاتی-درسنامه- سروش اسماعیلی

تناوب

در زیر نوشته شده است:

تابع متناوب

اگر نمودار تابع طوری باشد که همواره قسمتی از نمودار به طور منظم تکرار شود، به آن تابعی متناوب و به کوچکترین فاصله‌ای که تابع در آن تکرار می‌شود، دوره تناوب میگویند.

vدر تعریف ریاضی تابع f را متناوب میگوییم هرگاه عدد حقیقی مثبت T موجود باشد به طوری که:

x∈Df , x+T∈Df    =>  f (x+T)=f (x)

کوچکترین مقدار T همان دوره تناوب است.

نمودار شناسی مثلثاتی

•توابع به شکل y=asin(bx)+c و  y=acos(bx)+c دارای ماکزیمم |a|+c و مقدار مینیمم |a|-c میباشند.

•در تابع y=asin(bx)+c اگر a,b هم علامت باشند آنگاه نمودار با شروع از x=0 صعودی شروع میشود و برعکس.

•در تابع y=acos(bx)+c اگر a مثبت باشد آنگاه نمودار با شروع از x=0 نزولی شروع میشود و برعکس(b در اینجا تاثیر ندارد).

با دانستن این نکات به همراه نکات تناوب توابع میتوانیم ضابطه نمودار مثلثاتی را از روی شکل حدس بزنیم:

مثال) معادله منحنی y= acos(bx)+c   به صورت روبرو است آنرا بیابید.

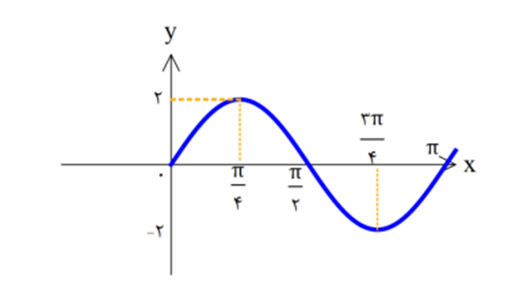
Max=2=|a|+c  c=0

Min=-2=-|a|+c  |a|=2

T=π= 2π/(|a|) => |a|=2      شروع صعودی=> a=-2

f(π/4)=2 => 2cos(bπ/4)=2 => cos(bπ/4)=1 => bπ/4 =2kπ⇒b=8k

🔵برای مطالعه کامل درسنامه میتوانید جزوه را از فایل ضمیمه دانلود کنید 🔵 

🔵عضویت در کانال تلگرام کانون برترها🔵