چندضلعی - هندسه دهم - خلاصه نکات درسی - فاضل مهرآئین

در این مطلب قصد داریم مبحث چندضلعی از هندسه دهم را در قالب خلاصه نکات و تست جمع بندی کنیم.

سلام دوستان ! ✋

در این مطلب قصد داریم  مبحث چندضلعی را در قالب درسنامه و تست بررسی کنیم.

در این مطلب پنج تست از چندضلعی ها قرار دادیم .

 اگر سوالی از این مطلب دارید در قسمت کامنت ها از بنده بپرسید .

برای دریافت پاسخ تشریحی ، فایل اصلی سوالات را در قسمت فایل های ضمیمه دانلود کنید .

ضلع: هر یک از پاره خط هایی را که چند ضلعی را تشکیل داده اند، ضلع چند ضلعی می نامند.

دو ضلع مجاور: دو ضلع را که یکی از دو انتهای آن ها مشترک است، دو ضلع مجاور می نامند.

راس: نقطه مشترک دو ضلع مجاور را راس می نامند.

دو راس مجاور: دو راسی را که دو سر یک ضلع اند، دو راس مجاور می نامند. دو راس را که مجاور نباشند، دو راس غیر مجاور می نامند.

زاویه داخلی: زاویه ای را که با دو ضلع مجاور تشکیل شده است و به سمت داخل چند ضلعی است، زاویه داخلی چند ضلعی می نامند.

دو زاویه مجاور: دو زاویه داخلی چند ضلعی را که در ضلعی مشترک اند، دو زاویه مجاور می نامند.

n ضلعی: اگر چند ضلعی از n ضلع تشکیل شده باشد، آن را n ضلعی می نامند. هر چند ضلعی  دست کم سه ضلع و سه راس دارد.

چند ضلعی محدب: چند ضلعی است که اگر هر خطی را که ضلعی از چند ضلعی روی آن افتاده است رسم کنیم، بقیه نقطه های چند ضلعی در یک طرف آن واقع شود.

هر چند ضلعی را که محدب نباشد، مقعر می نامیم.

تمام زوایای هر چند ضلعی محدب کوچک تر از 180 درجه هستند و برعکس، یعنی اگر در یک چند ضلعی تمام زوایا کوچک تر از 180 درجه باشند، این چند ضلعی محدب است.

قطر: در چند ضلعی، هر پاره خط را که دو سرش دو راس غیر مجاور هستند را قطر می نامیم.

مثلث قطر ندارد، چون دو راس غیر مجاور ندارد.

تعداد قطر های هر n ضلعی برابر با n(n-3)/2 است.

متوازی الاضلاع: چهار ضلعی است که هر دو ضلع مقابل آن موازی اند. به عبارت دیگر اگر در شکل زیر AB  موازی با CD و ADموازی با BC ، آن گاه ABCD متوازی الاضلاع است و برعکس.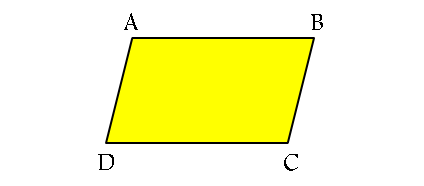

ویژگی های متوازی الاضلاع:

1) هر قطر متوازی الاضلاع آن را به دو مثلث هم نهشت تقسیم می کند. عکس این مطلب هم درست است. یعنی اگر هر یک از قطرهای چهار ضلعی آن را به دو مثلث هم نهشت تقسیم کند، این چهار ضلعی متوازی الاضلاع است.

2) در هر متوازی الاضلاع، اضلاع مقابل هم اندازه اند. عکس این مطلب هم درست است. یعنی اگر در یک چهار ضلعی هر دو ضلع مقابل هم اندازه باشند، این چهار ضلعی متوازی الاضلاع است.

3) در هر متوازی الاضلاع، هر دو زاویه مجاور مکمل اند و برعکس.

4) در هر متوازی اضلاع، هر دو زاویه مقابل هم اندازه اند و برعکس.

5) در هر متوازی اضلاع، قطرها یکدیگر را نصف می کنند و برعکس.

مستطیل: چهار ضلعی است که تمام زوایای آن قائمه اند. به عبارت دیگر،  اگر در شکل زیر تمام زوایا برابر با 90 درجه باشند، آن گاه ABCD مستطیل است و برعکس. هر مستطیل یک متوازی الاضلاع است و در نتیجه تمام ویژگی های یک متوازی الاضلاع را داراست. مستطیل متوازی الاضلاعی است که یک زاویه قائمه دارد.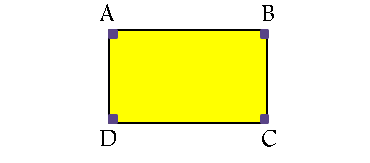

ویژگی های مستطیل:

1) در هر مستطیل قطرها برابرند.

2) اگر متوازی الاضلاعی دو قطر برابر داشته باشد، مستطیل است.

نکته: در هر مثلث قائم الزاویه، طول میانه وارد بر وتر، نصف وتر است و برعکس.

لوزی: چهار ضلعی است که طول هر چهار ضلع آن برابر است. به عبارت دیگر اگر در شکل زیر  AB=BC=CD=AD ، آن گاه ABCD لوزی است و برعکس. هر لوزی یک متوازی الاضلاع است و در نتیجه تمام ویژگی های یک متوازی الاضلاع را دارد. لوزی متوازی الاضلاعی است که دو ضلع مجاور برابر دارد.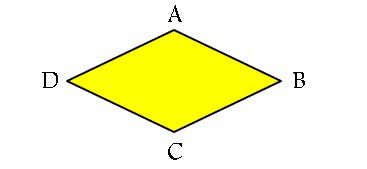

ویژگی های لوزی:

1) در لوزی، قطرها نیمساز زوایا هستند.

2) اگر قطرهای چهار ضلعی محدبی نیمساز زوایا باشند، آن چهارضلعی لوزی است.

3) در لوزی قطرها بر هم عمودند.

مربع: چهار ضلعی است که طول هر چهار ضلع آن برابر است و حداقل یک زاویه آن قائمه است. به عبارت دیگر اگر در شکل زیر AB=BC=CD=AD و A=90 ، آن گاه            مربع است و برعکس. در واقع می توان گفت که مربع، لوزی است که مستطیل است.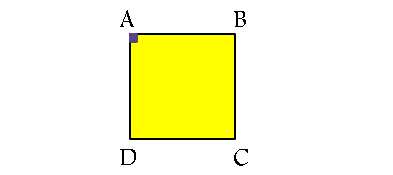

ویژگی های مربع:

1) مربع، لوزی است و در نتیجه تمام ویژگی های لوزی را دارد.

2) مربع، مستطیل است و در نتیجه تمام ویژگی های مستطیل را دارد.

تست ها 

1. در صفحه ای 15 نقطه وجود دارد که هیچ 3 تای آنها روی یک خط واقع نیستند. اگر بخواهیم تمام نقاط را با پاره خط هایی به هم وصل کنیم، به چند پاره خط نیاز داریم؟ 

1)90                    2)180                     3)105                     4)15

2. کدام یک از گزینه های زیر تعریف دقیقی از لوزی نیست؟

1) لوزی یک چهار ضلعی محدب است که قطرهایش نیمساز زوایا هستند.

2) لوزی یک متوازی الاضلاع است که قطرهایش نیمساز راس هایش هستند.

3) لوزی یک متوازی الاضلاع است که هر دو ضلع مجاورش با هم برابر هستند.

4) لوزی یک متوازی الاضلاع است که قطرهایش منصف یکدیگرند.

3. قطرهای متوازی الاضلاع زیر را رسم کرده ایم. طول قطر BD دو برابر ضلع BC است. با توجه به اندازه زوایای داده شده، اندازه زاویه D را مشخص کنید. 

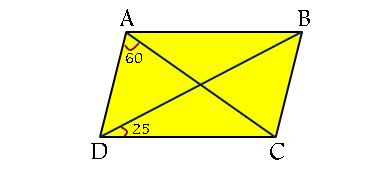
 1)85                     2)75                     3)65                     4)140

4. در مثلث قائم الزاویه شکل زیر، طول ضلع AC با طول میانه AM برابر است. همچنین DMB=3AMD. اندازه زاویه MDB کدام گزینه است؟

 1)30                     2)65                     3)70                       4)60

5. در مثلثی قائم الزاویه اندازه بین ارتفاع و میانه وارد بر وتر 30 درجه است. اندازه دو زاویه دیگر این مثلث قائم الزاویه کدام است؟

1) 30-60               2)10-80                 3) 5-85               4)40-50 

برای ارتباط بیشتر با برترها و رزرو پشتیبان ویژه، رتبه برترهای کانون قلمچی را دنبال کنید، 

همچنین می توانید با شماره ۰۲۱۸۴۵۱ داخلی ۳۱۲۳ تماس بگیرید.